题目内容
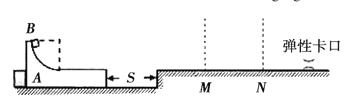
【题目】如图所示，质量为
的带有圆弧的滑块A静止放在光滑的水平面上，圆弧半径R=1.8m，圆弧的末端点切线水平，圆弧部分光滑，水平部分粗糙，A的左侧紧靠固定挡板，距离A的右侧S处是与A等高的平台，平台上宽度为L=0.5m的M、N之间存在一个特殊区域，B进入M、N之间就会受到一个大小为F=mg恒定向右的作用力。平台MN两点间粗糙，其余部分光滑，M、N的右侧是一个弹性卡口，现有一个质量为m的小滑块B从A的顶端由静止释放，当B通过M、N区域后碰撞弹性卡口的速度v不小于5m/s时可通过弹性卡口，速度小于5m/s时原速反弹，设m=1kg，g=10m/s2，求：
(1)滑块B刚下滑到圆弧底端时对圆弧底端的压力多大？
(2)若A、B间的动摩擦因数μ1=0.5，保证A与平台相碰前A、B能够共速，则S应满足什么条件？
(3)在满足(2)问的条件下，若A与B共速时，B刚好滑到A的右端，A与平台相碰后B滑上平台，设B与MN之间的动摩擦因数0＜μ＜1，试讨论因μ的取值不同，B在MN间通过的路程。
【答案】(1)30N；(2)S＞0.8m；(3)见解析
【解析】
(1)设B滑到A的底端时速度为v0，根据机械能守恒定律得
小球在圆弧底端合力提供向心力有
联立各式并代入数据得v0＝6m/s；FN＝30N。根据牛顿第三定律可知滑块对圆弧底端的压力为30N。
(2)设AB获得共同速度为v1，以向右为正方向，由动量守恒定律得
代入数据解得：v1=4m/s；对A应用动能定理得
代入数据解得：S=0.8m，即保证A与平台相碰前A、B能够共速，S应满足S＞0.8m。
(3)设B到达卡口的速度v2＝5m/s，B将从平台右侧离开，此时B与M、N的动摩擦因数为μ1，由动能定理得
解得：μ1=0.1，即0＜μ≤0.1，B从卡口右侧离开，通过的路程
S1＝L＝0.5m
如果B到达卡口的速度小于5m/s，B将被弹回，进入NM后做减速运动，到达M点速度恰好为零，设此时的动摩擦因数为μ2，则
解得μ2=0.8即0.1＜μ≤0.8，B从M左侧离开，通过的路程
如果0.8＜μ＜1，B经与卡口碰撞、往返多次后最终静止在N点，通过的路程S3，由动能定理得
解得
S3＝1.3μ（m）
