题目内容
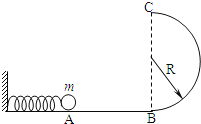
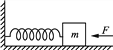
【题目】如图所示,光滑水平面MN的左端M处有一弹射装置P,右端N处与水平传送带理想连接.传送带水平部分长![]() =8m,并以恒定速度
=8m,并以恒定速度![]() =3m/s沿图示箭头方向移动.质量均为
=3m/s沿图示箭头方向移动.质量均为![]() =1kg、静止于MN上的物块A、B(视为质点)之间压缩一轻弹簧,贮有弹性势能
=1kg、静止于MN上的物块A、B(视为质点)之间压缩一轻弹簧,贮有弹性势能![]() =16J.若A、B与传送带间的动摩擦因数
=16J.若A、B与传送带间的动摩擦因数![]() ,则解除弹簧压缩,弹开物块A、B后,求:
,则解除弹簧压缩,弹开物块A、B后,求:

(1)物块B在传送带上向右滑行的最远距离![]() ;
;
(2)物块B返回到水平面MN时的速度![]() ;
;
(3)若物块B返回水平面MN后,与被弹射装置P弹回的物块A在水平面MN上弹性碰撞(碰撞过程无动能损失,碰撞时间极短),使物块B从传送带水平部分的右端Q滑出,则弹射装置P必须给物块A至少做多少功?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)解除锁定后弹簧恢复原长时,A、B的速度大小分别为![]() 、
、![]() ,由系统机械能守恒、动量守恒得:
,由系统机械能守恒、动量守恒得:
![]()
![]()
联立解得 ![]()
设B沿传送带向右滑行的最远距离为![]() ,由功能关系
,由功能关系
![]()
解得 ![]()
(2)因为![]() ,所以B返回时先加速再随传送带一起运动,B返回到水平面MN时的速度
,所以B返回时先加速再随传送带一起运动,B返回到水平面MN时的速度
![]()
(3)以A为研究对象,设被弹射装置P弹回的物块A的速度为![]() 由动能定理
由动能定理
![]()
B能从Q端滑出一定有![]()
设A与B弹性碰撞后,A、B的速度分别为![]() 、
、![]() ,有:
,有:
![]()
![]()
得![]()
(或直接写出A与B质量相等,完全弹性碰撞后速度互换,则A的速度
![]() )
)
联立解得 ![]() .
.

练习册系列答案
相关题目