题目内容
15. 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面的弹簧.在此过程中下面的木块移动的距离为( )
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面的弹簧.在此过程中下面的木块移动的距离为( )| A. | $\frac{{{m_1}g}}{k_1}$ | B. | $\frac{{{m_2}g}}{k_1}$ | C. | $\frac{{{m_1}g}}{k_2}$ | D. | $\frac{{{m_2}g}}{k_2}$ |
分析 开始时弹簧处于压缩状态,弹力等于两个木块的总重力,由胡克定律求出弹簧压缩的长度x1和x2.当上面的木块刚离开上面弹簧时,弹簧仍处于压缩状态,此时弹力等于下面木块的重力,再由胡克定律求出弹簧此时压缩的长度x2′,所以在这过程中下面木块移动的距离s2=x2-x2′.
解答 解:开始时:设上面弹簧压缩的长度x1下面弹簧压缩的长度x2,则有:
m1g=k1x1
m1g+m2g=k2x2
得到:${x}_{1}=\frac{{m}_{1}g}{{k}_{1}}$,${x}_{2}=\frac{({m}_{1}+{m}_{2})g}{{k}_{2}}$
当上面的木块刚离开上面弹簧时,设弹簧压缩的长度x2′,则有:
m2g=k2x2′
得到:${x}_{2}′=\frac{{m}_{2}g}{{k}_{2}}$
所以在这过程中下面木块移动的距离为:
${s}_{2}={x}_{2}-{x}_{2}′=\frac{{m}_{1}g}{{k}_{2}}$
故选:C
点评 本题考查处理含有弹簧的平衡问题能力,也可以直接由胡克定律根据$△x=\frac{F}{k}$求解形变量.

练习册系列答案
相关题目
6. 摩擦传动是传动装置中的一个重要模型,如图1历示的两个水平放置的轮盘靠摩擦力传动,其中O、O′分别为两轮盘的轴心,已知两个轮盘的半径比r甲:r乙=3:1,且在正常工作时两轮盘不打滑.今在两轮盘上分别放置两个同种材料制成的滑块A、B,两滑块与轮盘间的动摩擦因数相同,两滑块距离轴心O、O′的间距RA=2RB.若轮盘乙由静止开始缓慢地转动起来,且转速逐渐增加,则下列叙述正确的是( )
摩擦传动是传动装置中的一个重要模型,如图1历示的两个水平放置的轮盘靠摩擦力传动,其中O、O′分别为两轮盘的轴心,已知两个轮盘的半径比r甲:r乙=3:1,且在正常工作时两轮盘不打滑.今在两轮盘上分别放置两个同种材料制成的滑块A、B,两滑块与轮盘间的动摩擦因数相同,两滑块距离轴心O、O′的间距RA=2RB.若轮盘乙由静止开始缓慢地转动起来,且转速逐渐增加,则下列叙述正确的是( )
 摩擦传动是传动装置中的一个重要模型,如图1历示的两个水平放置的轮盘靠摩擦力传动,其中O、O′分别为两轮盘的轴心,已知两个轮盘的半径比r甲:r乙=3:1,且在正常工作时两轮盘不打滑.今在两轮盘上分别放置两个同种材料制成的滑块A、B,两滑块与轮盘间的动摩擦因数相同,两滑块距离轴心O、O′的间距RA=2RB.若轮盘乙由静止开始缓慢地转动起来,且转速逐渐增加,则下列叙述正确的是( )
摩擦传动是传动装置中的一个重要模型,如图1历示的两个水平放置的轮盘靠摩擦力传动,其中O、O′分别为两轮盘的轴心,已知两个轮盘的半径比r甲:r乙=3:1,且在正常工作时两轮盘不打滑.今在两轮盘上分别放置两个同种材料制成的滑块A、B,两滑块与轮盘间的动摩擦因数相同,两滑块距离轴心O、O′的间距RA=2RB.若轮盘乙由静止开始缓慢地转动起来,且转速逐渐增加,则下列叙述正确的是( )| A. | 滑块A和B在与轮盘相对静止时,角速度之比为ω甲:ω乙=1:3 | |
| B. | 滑块A和B在与轮盘相对静止时,向心加速度的比值为aA:aB=2:9 | |
| C. | 转速增加后滑块B先发生滑动 | |
| D. | 转速增加后两滑块一起发生滑动 |
3. 如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.此过程中小球的重力势能( )
如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.此过程中小球的重力势能( )
 如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.此过程中小球的重力势能( )
如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.此过程中小球的重力势能( )| A. | 增加mgh | B. | 增加mg(H+h) | C. | 减少 mgH | D. | 减少mg(H+h) |
10.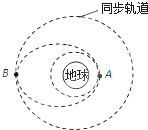 发射地球同步卫星时,先将卫星发射至距地面高度为h1的近地轨道上,在卫星经过A点时点火,实施变轨,进入远地点为B的椭圆轨道上,最后在B点再次点火,将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,则( )
发射地球同步卫星时,先将卫星发射至距地面高度为h1的近地轨道上,在卫星经过A点时点火,实施变轨,进入远地点为B的椭圆轨道上,最后在B点再次点火,将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,则( )
 发射地球同步卫星时,先将卫星发射至距地面高度为h1的近地轨道上,在卫星经过A点时点火,实施变轨,进入远地点为B的椭圆轨道上,最后在B点再次点火,将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,则( )
发射地球同步卫星时,先将卫星发射至距地面高度为h1的近地轨道上,在卫星经过A点时点火,实施变轨,进入远地点为B的椭圆轨道上,最后在B点再次点火,将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,则( )| A. | 卫星在近地圆轨道的周期最大 | |
| B. | 卫星在椭圆轨道上由A到B的过程速率逐渐减小 | |
| C. | 卫星在近地点A的加速度为$\frac{g{R}^{2}}{(R+{h}_{1})^{2}}$ | |
| D. | 远地点B距地表距离为($\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}$)${\;}^{\frac{1}{3}}$ |
20.如图是某质点运动的v-t图象,由图象倒得的正确结果是( )


| A. | 0~2s内的位移大小是3m | |
| B. | 0~4s内的平均速度是2m/s | |
| C. | 0~1s内的加速度大小大于2~4s内的加速度大小 | |
| D. | 0~1s内的运动方向与2~4s内的运动方向相反 |
4.已知月球半径为R,飞船在距月球表面高度为R的圆轨道上飞行,周期为T,万有引力常量为G,下列说法正确的是( )
| A. | 月球表面重力加速度为g=$\frac{32{π}^{2}R}{{T}^{2}}$ | |
| B. | 月球第一宇宙速度为$\frac{4πR}{T}$ | |
| C. | 月球密度为$\frac{3π}{G{T}^{2}}$ | |
| D. | 月球质量为$\frac{24π}{G{T}^{2}}$ |
5.用同一刻度尺去测量两个长度不同的物体时,( )
| A. | 测量较长的物体产生的绝对误差较大 | |
| B. | 测量较短的物体产生的绝对误差较大 | |
| C. | 测量较长的物体产生的相对误差较大 | |
| D. | 测量较短的物体产生的相对误差较大 |
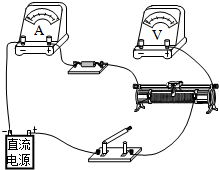 某研究性学习小组为了制作一个传感器,需要选用某种电学元件.实验中首先要描绘该元件的伏安特性曲线,实验室备有下列器材:
某研究性学习小组为了制作一个传感器,需要选用某种电学元件.实验中首先要描绘该元件的伏安特性曲线,实验室备有下列器材: