题目内容
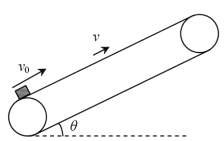
【题目】如图所示，一个足够长的传送带与水平面之间的夹角θ=30°，传送带在电动机的带动下以v=5m/s的速度向上匀速运动。一质量为1kg的物体以v0=10m/s的初速度从传送带底端向上运动，已知物体与传送带之间的动摩擦因数为μ=
，重力加速度g=10m/s2。
（1）求物体在传送带底端时的加速度
（2）求物体沿传送带向上运动的最大距离；
（3）若传送带向上匀速运动的速度(v)的大小可以调节，物体的初速度不变，当传送带的速度调节为多大时，物体从底端运动到最高点的过程中产生的热量最小?最小值是多大?
【答案】（1）
（2）10m（3）2.5m/s；12.5J
【解析】由于
，所以物体开始时受到的摩擦力向下，由牛顿第二定律可知
解得： 
，方向沿传送带向下
（2）
，所以物体减速到v后不能与传送带相对静止，物体从速度
减到v的过程中，向上运动的距离
然后物体减速到零的过程中
所以上升的最大距离为10m
（3）以传送带为参考系，物体向上减速运动的两个过程相对传送带的位移大小分别为
； 
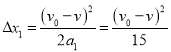物体向上运动产生的热量为
故当
时，Q最小
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
