题目内容
如图所示,小车B静止于水平轨道上,其左端固定一根劲度系数为K的轻弹簧,小车B的质量为m2.小车A的质量为m1,从高出水平轨道h处由静止开始沿曲轨道滑下,在水平轨道上与小车B发生相互作用.若轨道是光滑的,则弹簧压缩量最大时,A车的速度vA和弹簧的弹性势能Ep分别为( )

A.vA=
| ||||||
B.vA=
| ||||||
C.vA=
| ||||||
D.vA=
|

(1)设A小车到达圆弧底端时的速度为v0,
根据机械能守恒定律有:m1gR=
m1
①,
当A、B两小车速度相同时,弹簧的弹性势能最大,设共同速度为v
根据动量守恒定律有:m1v0=(m1+m2)vA ②,
所以vA=
根据机械能守恒定律有:EP=
m1
-
(m1+m2)
③,
联立①②③解得:EP=
所以正确的选项是B.
故选:B
根据机械能守恒定律有:m1gR=
| 1 |
| 2 |
| v | 20 |
当A、B两小车速度相同时,弹簧的弹性势能最大,设共同速度为v
根据动量守恒定律有:m1v0=(m1+m2)vA ②,
所以vA=
m1
| ||
| m1+m2 |
根据机械能守恒定律有:EP=
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
| v | 2A |
联立①②③解得:EP=
| m1m2gh |
| m1+m2 |
所以正确的选项是B.
故选:B

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,小车B静止于水平轨道上,其左端固定一根劲度系数为K的轻弹簧,小车B的质量为m2.小车A的质量为m1,从高出水平轨道h处由静止开始沿曲轨道滑下,在水平轨道上与小车B发生相互作用.若轨道是光滑的,则弹簧压缩量最大时,A车的速度vA和弹簧的弹性势能Ep分别为( )
如图所示,小车B静止于水平轨道上,其左端固定一根劲度系数为K的轻弹簧,小车B的质量为m2.小车A的质量为m1,从高出水平轨道h处由静止开始沿曲轨道滑下,在水平轨道上与小车B发生相互作用.若轨道是光滑的,则弹簧压缩量最大时,A车的速度vA和弹簧的弹性势能Ep分别为( ) 如图所示,小车B静止于水平轨道上,其左端固定一根劲度系数为K的轻弹簧,小车B的质量为m2.小车A的质量为m1,从高出水平轨道h处由静止开始沿曲轨道滑下,在水平轨道上与小车B发生相互作用.若轨道是光滑的,则弹簧压缩量最大时,A车的速度vA和弹簧的弹性势能Ep分别为( )
如图所示,小车B静止于水平轨道上,其左端固定一根劲度系数为K的轻弹簧,小车B的质量为m2.小车A的质量为m1,从高出水平轨道h处由静止开始沿曲轨道滑下,在水平轨道上与小车B发生相互作用.若轨道是光滑的,则弹簧压缩量最大时,A车的速度vA和弹簧的弹性势能Ep分别为( )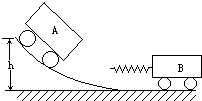 如图所示,小车B静止于光滑的水平轨道上,其左端固定一根劲度系数为K的弹簧,小车B及弹簧的总质量为m2,小车A的质量为m1,从高出水平轨道h处由静止开始沿光滑曲轨道滑下,在水平轨道上与小车B发生相互作用.则弹簧的最大弹性势能为
如图所示,小车B静止于光滑的水平轨道上,其左端固定一根劲度系数为K的弹簧,小车B及弹簧的总质量为m2,小车A的质量为m1,从高出水平轨道h处由静止开始沿光滑曲轨道滑下,在水平轨道上与小车B发生相互作用.则弹簧的最大弹性势能为

