��Ŀ����
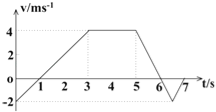
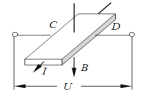
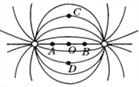
����Ŀ����ͼ����ʾ���߳�L=2.5m������m=0.5kg�������ν����߿��ڹ⻬��Ե��ˮƽ���ϣ�����װ�ô��ڷ�����ֱ���ϡ��Ÿ�Ӧǿ��ΪB=0.8T����ǿ�ų��У�����һ����ų��ı߽�MN�غϡ���ˮƽ��F�������£��߿��ɾ�ֹ��ʼ�����˶�������5s�������ų����˹��������õ�������������߿��еĵ���ǿ��I��ʱ��t�仯��ͼ����ͼ����ʾ������������У�
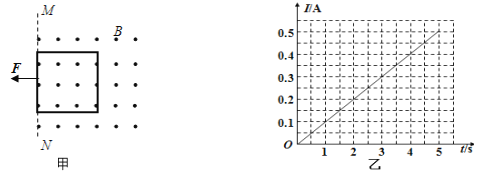
��1����ͼ�ҿɵó�ͨ���߿��߽���ĵ��Ϊ������I��t�Ĺ�ϵʽ��
��2������߿�ĵ���R��
��3�����ж�˵���߿���˶�����������ˮƽ��F��ʱ��t�仯�ı���ʽ��
���𰸡���1��1.25C�� ![]() ��2��4����3��
��2��4����3��![]()
����������1��I-tͼ���������Χ���������ֵ�ϵ���ͨ���߿����ĵ����q�����У�
q=![]() ��0.5��5C=1.25C
��0.5��5C=1.25C
��I-tͼ���֪����Ӧ����I��ʱ��t�����ȣ��У�I=kt=0.1t A
��2����![]() ��
�� ![]() ������=BL2��q=
������=BL2��q=![]() ��t
��t
�����ã� ![]()
����裺 ![]() ��
��
��3������ijʱ��t���߿���ٶ�Ϊv�����߿��и�Ӧ������ ![]()
��ϣ�1����I=kt=0.1t�ɵý������ٶ���ʱ��Ҳ�����Ա仯�ģ���![]()
���Կ�֪�߿����ȼ���ֱ���˶������ٶ�Ϊ��a=0.2m/s2
��ţ�ٵڶ����ɵã�F-BIL=ma��
�������ˮƽ��F��ʱ��t�仯���㣺F=��BLk��t+ma=��0.2t+0.1��N��

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�