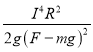题目内容
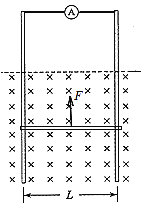
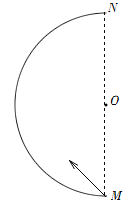
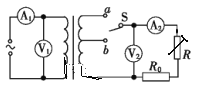
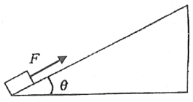
【题目】如下图所示,在倾角为θ=37°的足够长的固定斜面底端有一质量m=2.0kg的物体,物体与斜面间动摩擦因数μ=0.25.现用轻细绳将物体由静止沿斜面向上拉动,拉力F=20N,方向平行斜面向上,经时间t1=4s绳子突然断了,(sin37°=0.60,cos37°=0.80,g=10m/s2) 求:
(1)绳断时物体的速度大小;
(2)绳子断后物体还能沿斜面向上滑多远?
(3)从绳子断后物体回到出发点所用的总时间是多少?
【答案】(1)8m/s(2)4m(3)4.2s
【解析】
(1)物体向上运动过程中,由牛顿第二定律得:
F-mgsinθ-μmgcosθ=ma1
代入解得:
a1=2m/s2
绳断时物体的速度大小:
v1=a1t1=2×4=8m/s;
(2)绳断时,物体距斜面底端:
![]()
断绳后,物体向上运动过程中,由牛顿第二定律得:
mgsinθ+μmgcosθ=ma2
代入数据解得:
a2=8m/s2
物体做减速运动时间:
![]()
减速运动位移:
![]()
(3)物体沿斜面向下运动过程中,由牛顿第二定律得:
mgsinθ-μmgcosθ=ma3
代入数据解得:
a3=4m/s2
由速度时间关系公式可知,物体下滑到底端时位移为x=x1+x2=20m
根据![]() 解得
解得
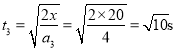
则从绳子断后物体回到出发点所用的总时间是
![]()

【题目】实验小组做“探究弹力与弹簧伸长量的关系"的实验,实验时,先把弹簧平放在桌面上,用直尺测出弹簧的原长L0=4.5cm,再把弹簧竖直悬挂起来,在下端挂钩码,每增加一只钩码记下对应的弹簧长度L,数据记录如下表所示:
钩码个数 | 1 | 2 | 3 | 4 | 5 |
弹力F/N | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 |
弹簧的长度L/cm | 7.0 | 9.0 | 11.0 | 13.0 | 15.0 |
(1)根据表中数据在图中作出F-L图线_______;
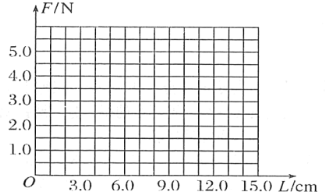
(2)由此图线可得,该弹簧劲度系数k=________N/m.
(3)图线与轴的交点坐标大于![]() 的原因是____。
的原因是____。