题目内容
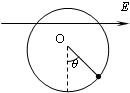如图所示，水平方向的匀强电场中，有一质量为m的带电小球，用长为l的细线悬于点O，当小球平衡时，细线和竖直方向的夹角为θ，现给小球一个初速度，速度方向和细线垂直，使小球恰能在竖直平面内做圆周运动，则圆周运动过程中速度的最小值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
分析：对小球受力分析，求出小球受到的电场力与重力的合力，小球恰好完成圆周运动，在在平衡位置的反方向上，小球做圆周运动的向心力由重力与电场力的合力提供，此时小球速度最小，由牛顿第二定律可以求出最小速度．
解答：解：以小球为研究对象，受重力与电场力，所以求出二力的合力：
F=
，电场力为mgtanθ，
由于小球恰好做圆周运动，所以圆周运动过程中速度的最小值处在重力和电场力合力的反方向上，且二力的合力提供向心力．
由牛顿第二定律得：
=m
，小球的最小速度v=
，故ABD错误，C正确．
故选：C．
F=
| mg |
| cosθ |
由于小球恰好做圆周运动，所以圆周运动过程中速度的最小值处在重力和电场力合力的反方向上，且二力的合力提供向心力．
由牛顿第二定律得：
| mg |
| cosθ |
| v2 |
| l |
|
故选：C．
点评：对小球受力分析，求出电场力与合力，由牛顿第二定律即可正确解题，此题可以把二力的合力视为等效场，求出等效重力加速度，在等效重力加速度的反方向上时，速度最小．
练习册系列答案
阅读快车系列答案
相关题目
（2010?上海模拟）如图所示，水平方向的平行线表示匀强电场的电场线，但未标明方向．电场中有一个带正电荷的微粒，电量为10-5 C，若该带电微粒仅受电场力的作用，从M点运动到N点时，动能减少了10-3 J，则该电荷运动轨迹应为虚线
如图所示，水平方向的匀强电场和匀强磁场互相垂直，竖直的绝缘杆足够长，杆上套一带电小环，小环和竖直杆都不光滑，小环由静止开始下落的过程中（ ）
如图所示，水平方向的匀强电场的场强为E，场区宽度为L，紧挨着电场的是垂直纸面向外的两个匀强磁场区域，其磁感应强度分别为B和2B，三个场的竖直方向均足够长．一个质量为m，电量为q的带正电粒子，其重力不计，从电场的边界MN上的a点由静止释放，经电场加速后进人磁场，穿过中间磁场所用的时间t0=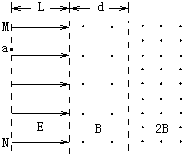
如图所示，水平方向的匀强电场的场强为E，电场区宽度为L，竖直方向足够长，紧挨着电场的是垂直纸面向外的两个匀强磁场区域，其磁感应强度分别为B和2B．一个质量为m、电量为q的带正电的粒子（不计重力）从电场的边界MN上的a点由静止释放，经电场加速后进入磁场，经过tB=πm/4qB 时间穿过中间磁场，进入右边磁场，然后按某一路径再返回到电场的边界MN上的某一点b（虚线为场区的分界面），求：