��Ŀ����
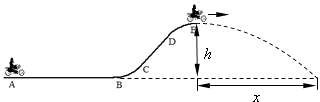
����Ŀ����ͼ��ʾ���綯����������B����ת�����ڹ��ֵ������£��������˴����A������Ǧ�=30����㹻��б���ϲ�����������B��б��ײ�A�ľ���ΪL=6.5m���������˵��¶��˶���B��ʱ�����������������Ӵ������������������������ջ᷵��б��ײ����뵲����ײ��������ֹ��������ʱ���������ٴ�ѹ���ˣ��ֽ������˴��������б���ϲ�������ܶ���ʼ����֪���ֱ�Ե���ٶȺ�Ϊv=4m/s�����ֶԸ˵���ѹ��FN=2��104N��������˼�Ķ�Ħ������Ϊ��=0.45���˵�����Ϊm=1��103Kg�����Ƹ���б����Ħ����ȡg=10m/s2 �� ��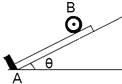
��1���ڹ��ֵ������£��˼��������ļ��ٶȣ�
��2���˼���������������ٶ���ͬʱǰ���ľ��룻
��3���˴���˿�ʼ�������ٴλص���˾�����ʱ�䣮
���𰸡�
��1���⣺�˼�������ʱ�������ܵ�Ħ���� f=��FN=0.45��2��104N=9��103N
����ţ�ٵڶ����ɵø˼��������ļ��ٶ� a= ![]() =
= ![]() m/s2=4m/s2
m/s2=4m/s2
���ڹ��ֵ������£��˼��������ļ��ٶ�Ϊ4m/s2��
��2���⣺�˼���������������ٶ���ͬʱǰ���ľ��� s= ![]() =
= ![]() m=2m
m=2m
�𣺸˼���������������ٶ���ͬʱǰ���ľ���Ϊ2m��
��3���⣺�ȼ���ʱ�� t1= ![]() =
= ![]() s=1s
s=1s
����ʱ�� t2= ![]() =
= ![]() s=1.25s
s=1.25s
��������˻ص���Ͷ˹��̣������ȱ����˶���a��=gsin��
��L=v0t�� ![]() at2
at2
��6.5=��4t3�� ![]() ��5t32
��5t32
��ã�t3=2.6s
�� T=t1+t2+t3=1s+1.25s+2.6s=4.725s��
�𣺸˴���Ͷ˿�ʼ�������ٴλص���Ͷ˾�����ʱ��Ϊ4.725s��
����������1���˼�������ʱ���ܵ���б�����ϵ�Ħ������������֧����������ţ�ٵڶ���������˼��������ļ��ٶȣ�
��2�������ȱ���ֱ���˶����ٶ�λ�ƹ�ʽ����˼���������������ٶ���ͬʱǰ���ľ��룮
��3���������������������������ȼ���ֱ���˶�����������ֱ���˶���������ֺ��������ȼ���ֱ���˶����������ȼ���ֱ���˶��������˶�ѧ��ʽ������������е��˶�ʱ�䣮
�����㾫����������Ŀ����֪�����������ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ���ȱ����˶��е�ƽ���ٶȵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ�����ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ��ƽ���ٶȣ�V=V0+Vt��

 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�