题目内容
【题目】如图所示，有一竖直平面直角坐标系，Oy竖直向上，在二、三象限存在垂直纸面向里的匀强磁场，磁感应强度为B；在一、四象限存在竖直向上的匀强电场，在一光滑绝缘、长为l的空心细管中，有一可视为质点的带电小球N，管的右端开口，小球初始位置坐标为（-l，2l），小球和管均静止，现管获得沿y轴负方向的速度
做匀速运动，管口到达O点时小球从管中射出，且恰好做匀速直线运动，忽略小球对管运动的影响，重力加速度为g，求：
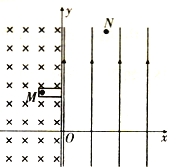
（1）小球从管中射出时，相对坐标系的速度；
（2）电场强度的大小；
（3）在管开始运动时，一个不带电，可视为质点的小球N，初始坐标为（2l，5l），同时由静止释放，恰与M相遇，写出
与l的关系式。
【答案】（1）
（2）
（3）
【解析】试题分析：小球在管中，水平做匀加速运动，竖直方向做匀速运动，根据速度的合成可得小球从管中射出时的速度；小球在电场中做匀速运动，则所受电场力和重力相等，小球在管中沿x方向做匀加速直线运动，结合运动学方程即可解题；N做自由落体运动，相遇即两球位置坐标相等，结合运动学方程即可解得速度与距离的关系式。
（1）由题意可得小球带正电，管向下运动的过程中，小球受到向右的洛伦兹： 
小球在竖直方向随管一起运动有： 
，小球从管中射出时：
水平方向： 
竖直方向： 
联立以上式解得： 
出射时小球的速度大小
方向：与x轴成
，斜向右下
（2）小球在电场中做匀速运动，则所受电场力和重力相等： 
小球在管中沿x方向做匀加速直线运动有： 
联立上式解得： 
解得： 
（3）N做自由落体运动，相遇即两球位置坐标相等，由题意得，小球射出后，向右水平移动2l，竖直移动2l
即相遇时N的竖直位移
对N有： 
解得： 
对M有： 
联立式可得： 
练习册系列答案
特高级教师点拨系列答案
相关题目
