题目内容
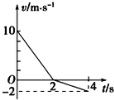
【题目】如图所示是一个质点做简谐运动的图象，根据图象回答下面的问题：
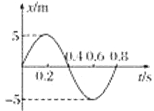
(1)振动质点离开平衡位置的最大距离；
(2)写出此振动质点的运动表达式；
(3)在0～0.6 s的时间内质点通过的路程；
(4)在t＝0.1 s、0.3 s、0.5 s、0.7 s时质点的振动方向；
(5)振动质点在0.6 s～0.8 s这段时间内速度和加速度是怎样变化的？
(6)振动质点在0.4 s～0.8 s这段时间内的动能变化是多少？
【答案】(1)5 cm (2)x＝5sin(2.5πt) cm (3)15 cm (4)正方向 负方向 负方向 正方向 (5)速度越来越大 加速度的方向指向平衡位置越来越小 (6)零
【解析】
x的最大值表示质点离开平衡位置的最大距离，即振幅；读出周期，求解角频率，即可写出振动方程；结合一个周期内振动的路程为4倍的振幅，根据图象的斜率等于速度，分析质点的速度方向即相应的动能变化。
(1)由振动图象可以看出，质点振动的振幅为5 cm，此即质点离开平衡位置的最大距离。
(2)由图象可知A＝5 cm，T＝0.8 s，φ＝0。所以x＝Asin(ωt＋φ)＝Asin(
t)＝5sin(
t) cm＝5sin(2.5πt) cm.
(3)由振动图象可以看出，质点振动的周期为T＝0.8s,0.6 s＝3×
，振动质点是从平衡位置开始振动的，故在0～0.6 s的时间内质点通过的路程为s＝3×A＝3×5cm＝15 cm。
(4)在t＝0.1s时，振动质点处在位移为正值的某一位置上，但若从t＝0.1s起取一段极短的时间间隔Δt(Δt→0)的话，从图象中可以看出振动质点的正方向的位移将会越来越大，由此可以判断得出质点在t＝0.1s时的振动方向是沿题中所设的正方向的．同理可以判断得出质点在t＝0.3 s、0.5 s、0.7s时的振动方向分别是沿题中所设的负方向、负方向和正方向。
(5)由振动图象可以看出，在0.6 s～0.8s这段时间内，振动质点从最大位移处向平衡位置运动，故其速度是越来越大的；而质点所受的回复力是指向平衡位置的，并且逐渐减小的，故其加速度的方向指向平衡位置且越来越小。
(6)由图象可以看出，在0.4s～0.8s这段时间内质点从平衡位置经过半个周期的运动又回到了平衡位置，尽管初、末两个时刻的速度方向相反，但大小是相等的，故这段时间内质点的动能变化为零。
