题目内容
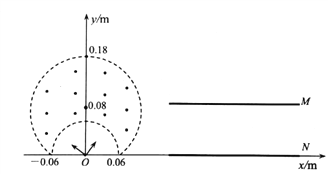
【题目】如图所示，半径r=0.06m的半圆形无场区的圆心在坐标原点O处，半径R=0.1m；磁感应强度大小B=0.075T的圆形有界磁场区的圆心坐标为（0，0.08m）；平行金属板MN的长度L=0.3m、间距d=0.1m，两板间加电压U=640V，其中N板收集粒子并全部中和吸收。一位于O点的粒子源向第I、II象限均匀发射比荷
=1×108C/kg、速度大小v=6×105m/s的带正电粒子，经圆形磁场偏转后，从第I象限射出的粒子速度方向均沿x轴正方向。不计粒子重力、粒子间的相互作用及电场的边缘效应，sin37°=0.6。
(1)粒子在磁场中运动的轨迹半径；
(2)求从坐标（0，0.18m）处射出磁场的粒子在O点入射方向与y轴的夹角；
(3)N板收集到的粒子占所有发射粒子的比例。
【答案】(1)0.08m（2）
（3）29%
【解析】试题分析：由洛伦兹力充当向心力可求得运动半径；做出带电粒子在磁场中做匀速圆周运动的轨迹，由几何知识即可求出θ；利用带电粒子在匀强电场中类平抛运动规律和带电粒子在磁场中的匀速圆周运动规律求。
（1）由洛伦兹力充当向心力： 
代入数据解得： 
（2）粒子运动轨迹如图所示：
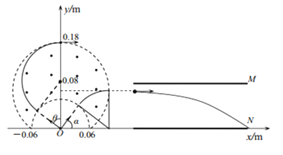
令从y=0.18m处出射的粒子对应的入射角方向与y轴的夹角为θ，由几何关系可得：
sinθ=0.8，即θ=530
（3）如上图所示，令恰能从下极板右端出射的粒子坐标为y，由带电粒子在电场中偏转的规律得： 
加速度为： 
飞行时间为： 
联立可得： 
设此粒子射入时与x轴的夹角为α，则由几何知识得： 
可得： 
，即
N板收集到的粒子占所有发射粒子的比例为： 
练习册系列答案
备战中考寒假系列答案
相关题目
