题目内容

相距2L的AB、CD两平行直线间区域存在着两个方向相反的匀强电场，其中PT上方的电场E1竖直向下；下方的电场E0竖直向上．PQ上连续分布着电量+q、质量m的粒子，依次以相同的初速度v0垂直射入E0中，PQ=L．若从Q点射入的粒子恰从M点水平射出（如图），MT=L/2．不计粒子的重力及相互作用．问：
（1）E0与E1的大小
（2）若从M点射出的粒子恰从中点S位置垂直射入边长为a的正方形有界匀强磁场区域（如图）．要使粒子能够从最上边界射出磁场区域．则该匀强磁场的磁感强度B大小？
分析：（1）粒子在两电场中做类平抛运动，由图可得出粒子在两电场中的运动情况；分别沿电场方向和垂直电场方向列出物理规律，联立可解得电场强度的大小；
（2）粒子进入磁场时做圆周运动，由题意可知其运动的临界半径值，再由牛顿第二定律可求得磁感应强度．
解答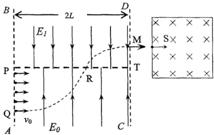：解：（1）设粒子在E0和E1中的时间为t1与t2，到达R时竖直速度为vy，则有L=
1
2
a1t
 
2
1
=
1
2
qE0
m
t
2
1
与
L
2
=
1
2
a2t
 
2
2
=
1
2
qE1
m
t
2
2

vy=
qE0
m
t1=
qE1
m
t2与v0（t1+t2）=2L
联立得E1=2E0即E0=
9m
v
2
0
8qL
与E1=
9m
v
2
0
4qL

（2）粒子进入磁场的速度为v0
若粒子恰好从最左上角偏离，则
R1=
a
2
=
mv0
qB1

得B1=
2mv0
qa

若粒子恰好从最右上角偏离，则
R
2
2
=a2+(R2-
a
2
)2
得R2=
5
4
a=
mv0
qB2

即B2=
4mv0
5qa

综合得
4mv0
5qa
＜B＜
2mv0
qa

答：（1）E0大小为
9m
v
2
0
8qL
，E1的大小为
9m
v
2
0
4qL
；（2）匀强磁场的磁感强度
4mv0
5qa
＜B＜
2mv0
qa
．
点评：带电粒子在电场磁场中的运动要把握其运动规律，在电场中利用几何关系得出其沿电场．和垂直于电场的运动规律；而在磁场中也是要注意找出相应的几何关系，从而确定圆心和半径
练习册系列答案
相关题目
（2008?佛山二模）如图所示，相距2L的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场，其中PT上方的电场E1的场强方向竖直向下，PT下方的电场E0的场强方向竖直向上，在电场左边界AB上宽为L的PQ区域内，连续分布着电量为+q、质量为m的粒子．从某时刻起由Q到P点间的带电粒子，依次以相同的初速度v0沿水平方向垂直射入匀强电场E0中，若从Q点射入的粒子，通过PT上的某点R进入匀强电场E1后从CD边上的M点水平射出，其轨迹如图，若MT两点的距离为
L2
．不计粒子的重力及它们间的相互作用．
试求：
（1）电场强度E0与E1；
（2）有一边长为a、由光滑绝缘壁围成的正方形容器，在其边界正中央开有一小孔S，将其置于CD右侧，若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中．欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出（粒子与绝缘壁碰撞时无能量和电量损失），并返回Q点，在容器中现加上一个如图所示的匀强磁场，粒子运动的半径小于a，磁感应强度B的大小还应满足什么条件？
如图所示，相距2L的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场，其中PT上方的电场E1的场强方向竖直向下，PT下方的电场E0的场强方向竖直向上，在电场左边界AB上宽为L的PQ区域内，连续分布着电量为+q、质量为m的粒子．从某时刻起由Q到P点间的带电粒子，依次以相同的初速度v0沿水平方向垂直射入匀强电场E0中，若从Q点射入的粒子，通过PT上的某点R进入匀强电场E1后从CD边上的M点水平射出，其轨迹如图，若MT两点的距离为
L2
．不计粒子的重力及它们间的相互作用．试求：
（1）电场强度E0与E1；
（2）在PQ间还有许多水平射入电场的粒子通过电场后也能垂直CD边水平射出，这些入射点到P点的距离有什么规律？
（2009?宜昌模拟）如图所示，相距2L的AB、CD两直线间的区域存在着两个方向相下方的电场界匀强电场，其中PT上方的电场E1竖直向下，下方的电场E0竖直向上，PQ上连续分布着电量为+q、质量为m的粒子，依次以相同的初速度v0．垂直射入E0中，PQ=L．若从Q点射入的粒子恰从M点水平射出，其轨迹如图，MT=
L2
．不计粒子的重力及它们间的相互作用．试求：
（1）E0与E1的大小；
（2）若从M点射出的粒子恰从中点S孔垂直射入边长为a的正方形容器中，容器中存在如图所示的匀强磁场，已知粒子运动的半径小于a．欲使粒子与器壁多次垂直碰撞后仍能从S孔射出（粒子与绝缘壁碰撞时无能量和电量损失），求磁感应强度B应满足的条件？
（3）在PQ间还有许多水平射入电场的粒子通过电场后也能从CD边水平射出，这些入射点到P点的距离应满足的条件？

如图所示，相距2L的AB、CD两直线间存在着两个大小不同、方向相反的有界匀强电场，其中PT上方的电场E1方向竖直向下，PT下方的电场E0方向竖直向上，在电场左边界AB上宽为L的PQ区域内，连续分布着电荷量为+q、质量为m的粒子。从某时刻起由Q到P点间的带电粒子，依次以相同的初速度v0沿水平方向垂直射入匀强电场E0中，若从Q点射入的粒子，通过PT上的某点R进入匀强电场E1后从CD边上的M点水平射出，其轨迹如图所示，测得MT两点的距离为L/2。不计粒子重力及它们间的相互作用。试求：(m、q、L,、a、 v0为已知量)

1.电场强度E0的大小 ；

2.在PQ间还有许多水平射入电场的粒子通过电场后也能垂直CD边水平射出，这些入射点到P点的距离有什么规律?

3.有一边长为a、由光滑绝缘壁围成的正方形容器，在其边界正中央开有一小孔S，将其置于CD右侧，若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中。欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无能量和电量损失)，并返回Q点，在容器中现加上一个如图所示的匀强磁场，粒子运动的半径小于a，磁感应强度B的大小还应满足什么条件？

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网