题目内容
(2008?佛山二模)如图所示,相距2L的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场,其中PT上方的电场E1的场强方向竖直向下,PT下方的电场E0的场强方向竖直向上,在电场左边界AB上宽为L的PQ区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起由Q到P点间的带电粒子,依次以相同的初速度v0沿水平方向垂直射入匀强电场E0中,若从Q点射入的粒子,通过PT上的某点R进入匀强电场E1后从CD边上的M点水平射出,其轨迹如图,若MT两点的距离为
.不计粒子的重力及它们间的相互作用.
试求:
(1)电场强度E0与E1;
(2)有一边长为a、由光滑绝缘壁围成的正方形容器,在其边界正中央开有一小孔S,将其置于CD右侧,若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中.欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无能量和电量损失),并返回Q点,在容器中现加上一个如图所示的匀强磁场,粒子运动的半径小于a,磁感应强度B的大小还应满足什么条件?

| L | 2 |
试求:
(1)电场强度E0与E1;
(2)有一边长为a、由光滑绝缘壁围成的正方形容器,在其边界正中央开有一小孔S,将其置于CD右侧,若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中.欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无能量和电量损失),并返回Q点,在容器中现加上一个如图所示的匀强磁场,粒子运动的半径小于a,磁感应强度B的大小还应满足什么条件?

分析:(1)粒子在两电场中做类平抛运动,由图可得出粒子在两电场中的运动情况;分别沿电场方向和垂直电场方向列出物理规律,联立可解得电场强度的大小;
(2)粒子进入磁场时做圆周运动,由题意可知其运动的临界半径值,再由牛顿第二定律可求得磁感应强度.
(2)粒子进入磁场时做圆周运动,由题意可知其运动的临界半径值,再由牛顿第二定律可求得磁感应强度.
解答:解:(1)设粒子经PT直线上的点R由E0电场进入E1电场,由Q到R及R到M点的时间分别为t1与t2,到达R时竖直速度为vy,
则:由s=
at2
v=at
及牛顿第二定律,F=qE=ma
得:L=
a1
=
①
而
=
a2
=
②
速度关系,vy=
t1=
t2③
v0(t1+t2)=2L④
上述三式联立解得:E1=2E0,
E0=
即E1=
.
(3)欲使粒子仍能从S孔处射出,粒子的运动轨迹可能是如图甲、乙所示的两种情况
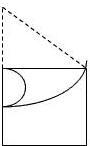 甲S对图甲所示的情形,粒子运动的半径为R1,
甲S对图甲所示的情形,粒子运动的半径为R1,
则R1=
,n=0、1、2、…
又qv0B1=
解得:B1=
,n=0、1、2、3…
S乙对图乙所示的情形,粒子运动的半径为R2,则R2=
,k=1、2、…
又qv0B2=
则有 B2=
,k=1、2、3…
综合B1、B2得:B=
,N=1、2、3…
或R=
,N=1、2、…
又qv0B2=
解得,B2=
,N=1、2、3…
答:(1)电场强度E0=
,E1=
.;
(2)粒子运动的半径小于a,磁感应强度B的大小还应满足的条件B2=
,N=1、2、3…
则:由s=
| 1 |
| 2 |
v=at
及牛顿第二定律,F=qE=ma
得:L=
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
| qE0 |
| m |
| t | 2 1 |
而
| L |
| 2 |
| 1 |
| 2 |
| t | 2 2 |
| 1 |
| 2 |
| qE1 |
| m |
| t | 2 2 |
速度关系,vy=
| qE0 |
| m |
| qE1 |
| m |
v0(t1+t2)=2L④
上述三式联立解得:E1=2E0,
E0=
9m
| ||
| 8qL |
即E1=
9m
| ||
| 4qL |
(3)欲使粒子仍能从S孔处射出,粒子的运动轨迹可能是如图甲、乙所示的两种情况
 甲S对图甲所示的情形,粒子运动的半径为R1,
甲S对图甲所示的情形,粒子运动的半径为R1,则R1=
| a |
| 2(2n+1) |
又qv0B1=
| mv02 |
| R1 |
解得:B1=
| 2(2n+1)mv0 |
| qa |
S乙对图乙所示的情形,粒子运动的半径为R2,则R2=
| a |
| 4k |
又qv0B2=
| mv02 |
| R2 |
则有 B2=
| 4kmv0 |
| qa |
综合B1、B2得:B=
| 2Nmv0 |
| qa |
或R=
| a |
| 2N |
又qv0B2=
| mv02 |
| R2 |
解得,B2=
| 2Nmv0 |
| qa |
答:(1)电场强度E0=
9m
| ||
| 8qL |
9m
| ||
| 4qL |
(2)粒子运动的半径小于a,磁感应强度B的大小还应满足的条件B2=
| 2Nmv0 |
| qa |
点评:带电粒子在电场磁场中的运动要把握其运动规律,在电场中利用几何关系得出其沿电场.和垂直于电场的运动规律;而在磁场中也是要注意找出相应的几何关系,从而确定圆心和半径.

练习册系列答案
相关题目
 (2008?佛山二模)用一轻绳将小球P系于光滑墙壁上的O点,在墙壁和球P之间夹有一矩形物块Q,如图所示.P、Q均处于静止状态,则下列相关说法正确的是( )
(2008?佛山二模)用一轻绳将小球P系于光滑墙壁上的O点,在墙壁和球P之间夹有一矩形物块Q,如图所示.P、Q均处于静止状态,则下列相关说法正确的是( )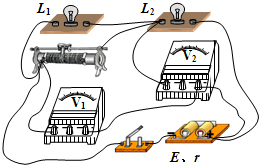 (2008?佛山二模)如图所示,电源电动势为E,内电阻为r.两电压表可看作是理想电表,当闭合开关,将滑动变阻器的触片由右端向左滑动时,下列说法中正确的是( )
(2008?佛山二模)如图所示,电源电动势为E,内电阻为r.两电压表可看作是理想电表,当闭合开关,将滑动变阻器的触片由右端向左滑动时,下列说法中正确的是( )