Question

（2009?宜昌模拟）如图所示，相距2L的AB、CD两直线间的区域存在着两个方向相下方的电场界匀强电场，其中PT上方的电场E₁竖直向下，下方的电场E₀竖直向上，PQ上连续分布着电量为+q、质量为m的粒子，依次以相同的初速度v₀．垂直射入E₀中，PQ=L．若从Q点射入的粒子恰从M点水平射出，其轨迹如图，MT=

L

2

．不计粒子的重力及它们间的相互作用．试求：
（1）E₀与E₁的大小；
（2）若从M点射出的粒子恰从中点S孔垂直射入边长为a的正方形容器中，容器中存在如图所示的匀强磁场，已知粒子运动的半径小于a．欲使粒子与器壁多次垂直碰撞后仍能从S孔射出（粒子与绝缘壁碰撞时无能量和电量损失），求磁感应强度B应满足的条件？
（3）在PQ间还有许多水平射入电场的粒子通过电场后也能从CD边水平射出，这些入射点到P点的距离应满足的条件？

Answer 1

分析：（1）粒子在两电场中做类平抛运动，由图可得出粒子在两电场中的运动情况；分别沿电场方向和垂直电场方向列出物理规律，联立可解得电场强度的大小；
（2）粒子进入磁场时做圆周运动，由题意可知其运动的临界半径值，再由牛顿第二定律可求得磁感应强度．
（3）设粒子第一次达PT直线用时△t，水平位移为△x，竖直位移为△y，推导出△x和△y与时间△t的关系式，再分两种情况进行讨论：1、若粒子从E₁电场垂直CD射出电场；2、若粒子从E0电场垂直CD射出电场．

解答：解：（1）设粒子在E₀和E₁的时间分别为t₁与t₂，到达R时竖直速度为v_y，则：
由s=

1

2

at²、v=at及F=qE=ma得：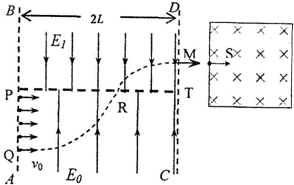
  L=

1

2

a₁t

2 1

=

1

2

qE 0

m

t

2 1

  ①
 

L

2

=

1

2

a2t

2 2

=

1

2

qE 1

m

t

2 2

  ②
 v_y=

qE0

m

t1=

qE1

m

t2   ③
  v₀（t₁+t₂）=2L　　④
上述三式联立得：E₁=2E₀，E₀=

9m v 2 0

8qL

即　E₁=

9m v 2 0

4qL

（2）欲使粒子仍能从S孔射出，粒子的运动轨迹是如图所示
的情形，粒子运动的半径为R₁
则　R₁=

a

2(2n+1)

，n=0，1，2…
又　qv₀B₁=

mv   2 0

R1

解得：B₁=

2(2n+1)mv0

qa

，n=0，1，2，3…
（3）由E₁=2E₀及③式可得t₁=2t₂ 　则PR=2RT
设粒子第一次达PT直线用时△t，水平位移为△x，则
△x=v₀△t
△y=

1

2

qE0

m

(△t) 2
讨论：
1、若粒子从E₁电场垂直CD射出电场，则
 （3n+1）△x+

△x

2

=2L　（n=0，1，2，3…）
得：△y=

1

2

qE0

m

(

△x

v0

) 2=

1

2

qE0

m

(

4L

3(2n+1)v0

) 2=

L

(2n+) 2

（n=0，1，2，3…）
2、若粒子从E0电场垂直CD射出电场，则
  3k△x=2L　（k=1、2、3、…）
得△y=

1

2

qE0

m

(

△x

v0

) 2=

1

2

qE0

m

(

2L

3kv0

) 2=

L

4k 2

（k=1、2、3、…）
答：
（1）E₀与E₁的大小分别为

9m v 2 0

8qL

和

9m v 2 0

4qL

；
（2）磁感应强度B应满足的条件是B₁=

2(2n+1)mv0

qa

，n=0，1，2，3…．
（3）在PQ间还有许多水平射入电场的粒子通过电场后也能从CD边水平射出，这些入射点到P点的距离应满足的条件是：
 1、若粒子从E₁电场垂直CD射出电场，则
△y=

1

2

qE0

m

(

△x

v0

) 2=

1

2

qE0

m

(

4L

3(2n+1)v0

) 2=

L

(2n+) 2

（n=0，1，2，3…）
 2、若粒子从E0电场垂直CD射出电场，则
△y=

1

2

qE0

m

(

△x

v0

) 2=

1

2

qE0

m

(

2L

3kv0

) 2=

L

4k 2

（k=1、2、3、…）．

点评：带电粒子在电场磁场中的运动要把握其运动规律，在电场中利用几何关系得出其沿电场．和垂直于电场的运动规律；而在磁场中也是要注意找出相应的几何关系，从而确定圆心和半径．