题目内容
(10分)如图所示，一固定的楔形木块，其斜面的倾角为θ＝30°，另一边与水平地面垂直，顶端有一个定滑轮，跨过定滑轮的细线 两端分别与物块A和B连接，A的质量为4m，B的质量为m.开始时，将B按在地面上不动，然后放开手，让A沿斜面下滑而B上升，所有摩擦均忽略不计．当A沿斜面下滑距离x后，细线突然断了．求物块B上升的最大高度H.(设B不会与定滑轮相碰)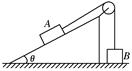
x
解析试题分析：设细线断前一瞬间A和B速度的大小为v，A沿斜面下滑距离x的过程中，A的高度降低了xsinθ，B的高度升高了x.物块A和B组成的系统机械能守恒，物块A机械能的减少量等于物块B机械能的增加量，即
4mgxsinθ－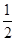
·4mv2＝mgx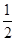＋mv2
细线断后，物块B做竖直上抛运动，物块B机械能守恒，设物块B继续上升的最大高度为h，
有mgh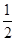＝mv2.
联立两式解得h＝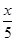
，故物块B上升的最大高度为H＝x＋h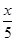＝x＋＝x.
考点：本题考查了机械守恒定律的应用
点评：根据机械能守恒的条件判断系统机械能是否守恒是关键，在确定守恒的条件下，更要明确在哪个过程中机械能守恒．
练习册系列答案
相关题目
冲上圆弧轨道，已知圆弧轨道的质量M=3m，不计摩擦和空气阻力，
，电动机M的内电阻为
，当开关s闭合，电动机转动稳定后，理想电压表的读数为
。若电动机除了内电阻外不计其他损耗。求:（1）电动机输出的机械功率P1.（2）电路消耗的总功率P。