题目内容
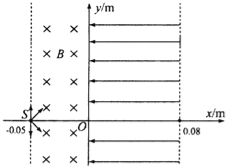
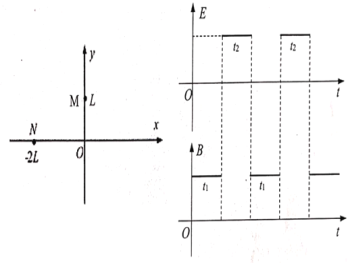
【题目】在xOy坐标中,有随时间周期性变化的电场和磁场(磁场持续t1后消失;紧接着电场出现,持续t2时间后消失,接着磁场......如此反复),如图所示,磁感应强度方向垂直纸面向里,电场强度方向沿y轴向下,有一质量为m,带电量为+q的带电粒子,在t=0时刻,以初速v0从0点沿x轴正方向出发,在t1时刻第一次到达y轴上的M (0,L)点,t1+t2时刻第一次回到x轴上的 N(-2L,0)点,不计粒子重力,t1、t2均未知。求:
(1)磁感应强度B和电场强度E的大小;
(2)粒子从0点出发到第二次回到x轴所用的时间;
(3)粒子第n次回到x轴的坐标。
【答案】(1) E=![]() (2) t总=
(2) t总=![]() (3) (-2L+
(3) (-2L+![]() L,0)
L,0)
【解析】
(1)粒子从O到M做圆周运动,半径:
R0=![]()
qBv0=![]()
B=![]()
M到N粒子在电场中运动:
2L=v0t2
L=![]()
a=![]()
![]()
(2)粒子从N做圆周运动,在N点vNy=at2,vNy=v0,速度方向与—x轴夹角为45°,vN=![]() ,所以做圆周运动的半径为:
,所以做圆周运动的半径为:
R1=![]()
而粒子在磁场中运动周期:T=![]() 与粒子速度无关,故经过时间t1粒子做半圆到P点,接下来只在电场力的作用下运动,P点速度方向与N点相反,所以从P到Q是M到N 的逆运动,有
与粒子速度无关,故经过时间t1粒子做半圆到P点,接下来只在电场力的作用下运动,P点速度方向与N点相反,所以从P到Q是M到N 的逆运动,有![]() ,得Q点刚好在x轴上(L,0)则从O点出发到第二次回到轴所需时间:
,得Q点刚好在x轴上(L,0)则从O点出发到第二次回到轴所需时间:
t总= 2(t1+t2)
又
t1=![]()
t2=![]()
得:
t总=![]()
(3)如图所示,粒子接下来做有规律的运动,到达x轴的横坐标依次为:
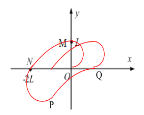
第一次:-2L
第二次:-2L+3L
第三次:-2L+3L-2L
…………
若n取偶数2,4,6......有:
![]() ,
,
坐标为(![]() ,0)
,0)
若n取奇数1,3,5........有:
-2L+![]() (-2L+3L)=-2L+
(-2L+3L)=-2L+![]() L,
L,
坐标为(-2L+![]() L,0)
L,0)

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目