Question

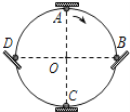
【题目】如图所示，自行车的小齿轮A、大齿轮B、后轮C是相互关联的三个转动部分，且半径RB=4RA、RC=8RA ， 如图所示．当自行车正常骑行时A、B、C三轮边缘的向心加速度的大小之比aA：aB：aC等于（ ）

A.1：1：8
B.4：1：4
C.4：1：32
D.1：2：4

Answer 1

【答案】C
【解析】解：由于A轮和B轮是皮带传动，皮带传动的特点是两轮与皮带接触点的线速度的大小与皮带的线速度大小相同，故：

vA=vB，

所以，vA：vB=1：1

由于A轮和C轮共轴，故两轮角速度相同，

即：ωA=ωC，

故：ωA：ωC=1：1

由角速度和线速度的关系式v=ωR可得：

vA：vC=RA：RC=1：8

所以，vA：vB：vC=1：1：8

又因为RA：RB：RC=1：4：8

根据a= 得：

aA：aB：aC=4：1：32

故答案为：C．
根据向心加速度和角速度，以极限速度的公式列方程进行分析。