题目内容
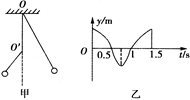
如图所示的单摆,摆球a向右摆动到最低点时,恰好与一沿水平方向向左运动的黏性小球b发生碰撞,并黏接在一起,且摆动平面不变.已知碰撞前a球摆动的最高点与最低点的高度差为h,摆动的周期为T,a球质量是b球质量的5倍,碰撞前a球在最低点的速度是b球速度的一半.则碰撞后( )


A.摆动的周期为 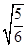 T T |
B.摆动的周期为  T T |
| C.摆球的最高点与最低点的高度差为0.3 h |
| D.摆球的最高点与最低点的高度差为0.25 h |
D
单摆周期T=2π 与摆球质量和摆角无关,故A?B都错.设a球碰撞前速率为va,碰后a?b共同速度为v,上升最大高度为h′,由机械能定守恒得magh=
与摆球质量和摆角无关,故A?B都错.设a球碰撞前速率为va,碰后a?b共同速度为v,上升最大高度为h′,由机械能定守恒得magh=
由碰撞过程中动量守恒得mava-mb(2va)=(ma+mb)v,
又(ma+mb)gh′= (ma+mb)v2,
(ma+mb)v2,
及ma=5mb,联立解得h′=0.25h,故D对.
 与摆球质量和摆角无关,故A?B都错.设a球碰撞前速率为va,碰后a?b共同速度为v,上升最大高度为h′,由机械能定守恒得magh=
与摆球质量和摆角无关,故A?B都错.设a球碰撞前速率为va,碰后a?b共同速度为v,上升最大高度为h′,由机械能定守恒得magh=
由碰撞过程中动量守恒得mava-mb(2va)=(ma+mb)v,
又(ma+mb)gh′=
 (ma+mb)v2,
(ma+mb)v2,及ma=5mb,联立解得h′=0.25h,故D对.

练习册系列答案
相关题目
 )和x2=9asin(8πbt+
)和x2=9asin(8πbt+ ),其中a、b为正的常数,则它们的:振幅之比为__________;摆长之比为_________。
),其中a、b为正的常数,则它们的:振幅之比为__________;摆长之比为_________。



 mv2
mv2
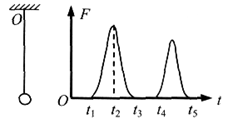

 。为了用图象法验证单摆周期T和最大摆角q的关系,他测出摆长为l的同一单摆在不同最大摆角q时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。
。为了用图象法验证单摆周期T和最大摆角q的关系,他测出摆长为l的同一单摆在不同最大摆角q时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。