题目内容
一个质量为m的物体静止放在光滑水平面上，在互成60°角的大小相等的两个水平恒力作用下，经过一段时间，物体获得的速度为v，在力的方向上获得的速度分别为v1、v2，那么在这段时间内，其中一个力做的功为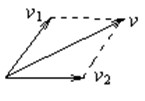 
A． | B． | C． | D． |
B
解析试题分析：大小相等，方向夹角为60°两个力的作用下，物体从静止运动到速度为v，则这两个力做的功一样多，且合力功为
，所以其中一个力做的功为总功的一半，即为
，故B正确；ACD错误；
故选：B
考点：考查了功的计算，运动的合成与分解
点评：无法用功的表达式计算，由动能定理可求出合力功，由于两力做功一样，因此可求出一个力做的功．
练习册系列答案
相关题目
在粗糙水平面上静放着一个质量为m的物体，知该物体与水平面之间的动摩擦因数为μ（设最大静摩擦力与滑动摩擦力相等）．现对该物体施加一个水平方向的变力F，其特点是：
①F=2μmg且作用t0时间；②F=μmg且作用t0时间；③F=0且历时t0．
若此外力F按以下顺序所对应的规律变化，则使该物体在3t0末速度最大的情况和在3t0时间内摩擦力做功数值最大的情况分别是（ ）
①F=2μmg且作用t0时间；②F=μmg且作用t0时间；③F=0且历时t0．
若此外力F按以下顺序所对应的规律变化，则使该物体在3t0末速度最大的情况和在3t0时间内摩擦力做功数值最大的情况分别是（ ）
| A、③①②、①②③ | B、②③①、①③② | C、③②①、②①③ | D、①②③、②③① |
一个质量为m的物体静止在倾角为α的斜面上，如图所示，物体与斜面间的最大静摩擦因数为2tanα，现给物体施加一个平行斜面底边的水平推力，至少要多大力才能把物体推动（ ）| A、mg sinα | ||
| B、mg cosα | ||
C、
| ||
| D、3mg sinα |