题目内容
19. 质量为m1=1.01kg和质量为m2(未知)的两个物体在光滑的水平面上发生正碰,碰撞时间不计,其位移x随时间t变化的图象如图所示,求:
质量为m1=1.01kg和质量为m2(未知)的两个物体在光滑的水平面上发生正碰,碰撞时间不计,其位移x随时间t变化的图象如图所示,求:(1)质量m2;
(2)质量为m1的物体在碰撞过程中动量变化量;
(3)通过计算说明,碰撞过程是弹性碰撞还是非弹性碰撞.
分析 (1)由图示图象求出物体的速度,碰撞过程动量守恒,应用动量守恒定律可以求出物体的质量;
(2)根据物体m1碰撞前后的动量,然后求出碰撞前后动量的变化;
(3)根据碰撞前后机械能是否守恒判断是否为弹性碰撞即可.
解答 解:(1)由图示图象可知,碰撞前m2是静止的,m1的速度为:v1=$\frac{{x}_{1}}{{t}_{1}}$=$\frac{8}{2}$=4m/s,
碰后m1的速度:v1′=$\frac{{x}_{1}′}{{t}_{1}′}$=$\frac{0-8}{6-2}$=-2m/s,
m2的速度:v2′=$\frac{{x}_{2}′}{{t}_{2}′}$=$\frac{16-8}{6-2}$=2m/s,
以m1的初速度方向为正方向,由动量守恒定律有:m1v1=m1v1′+m2v2′,
代入数据得:1×4=1×(-2)+m2×2,
解得:m2=3kg;
(2)质量为m1的物体在碰撞过程中动量的变化量是:
△p1=p1′-p1=1×(-2)-1×4=-6Kg•m/s,
负号表示动量的变化量方向与初速度方向相反.
(3)碰撞前总动能为:Ek=Ek1+Ek2=$\frac{1}{2}$m1v12=$\frac{1}{2}$×1×42+0=8J,
碰撞后总动能为:Ek′=Ek1′+Ek2′=$\frac{1}{2}$m1v1′2+$\frac{1}{2}$m2v2′2=$\frac{1}{2}$×1×22+$\frac{1}{2}$×3×22=8J,
则:Ek=Ek′,碰撞过程动能没有损失,则碰撞是弹性碰撞.
答:(1)质量m2为3kg;
(2)质量为m1的物体在碰撞过程中动量变化量大小是6Kg.m/s,动量的变化量方向与初速度方向相反.
(3)碰撞过程是弹性碰撞.
点评 本题主要考查了动量守恒定律得应用,要知道判断是否为弹性碰撞的方法是看机械能是否守恒,若守恒,则是弹性碰撞,若不守恒,则不是弹性碰撞.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
(1)为了验证小车的运动是匀变速运动,请进行下列计算,填入表内(单位:cm)
| X2-X1 | X3-X2 | X4-X3 | X5-X4 | X6-X5 | $\overline{△X}$ |
(2)根据匀变速直线运动的规律,可以求得物体的加速度a=$\frac{△x}{T^2}$=1.58m/s2.
(3)根据an-3=$\frac{{{x_n}-{x_{n-3}}}}{{3{T^2}}}$,可求出a1=$\frac{{{x_4}-{x_1}}}{{3{T^2}}}$=1.59m/s2,a2=$\frac{{{x_5}-{x_2}}}{{3{T^2}}}$=1.57m/s2,a3=$\frac{{{x_6}-{x_3}}}{{3{T^2}}}$=1.59m/s2,所以,$\overline a$=$\frac{{{a_1}+{a_2}+{a_3}}}{3}$=1.58m/s2.
| A. | “搓搓手就感觉手暖和些”是通过会热传递来改变物体内能 | |
| B. | 在热传递过程中,内能多的物体其内能将减少,内能少的物体其内能将增加,直到两个物体的内能相等 | |
| C. | 一个系统与另一个系统是否达到热平衡状态取决于温度 | |
| D. | 0℃水的内能比0℃的内能多 |
| A. | 天然放射现象的性现,揭示了原子具有复杂结构 | |
| B. | 汤姆生发现电子揭示了原子具有复杂结构,提出了原核工结构模型 | |
| C. | 玻尔的原子结构理论是在卢瑟福核式结构学说基础上引进了量子理论 | |
| D. | α射线、β射线、γ射线本质上都是电磁波 |
 氢原子的能级如图所示,一群氢原子处于n=3的激发态,在向基态跃迁的过程中,下列说法中正确的是( )
氢原子的能级如图所示,一群氢原子处于n=3的激发态,在向基态跃迁的过程中,下列说法中正确的是( )| A. | 这群氢原子能发出三种频率不同的光,其中从n=3跃迁到n=1所发出光的波长最短 | |
| B. | 这群氢原子能发出两种频率不同的光,其中从n=3跃迁到n=1所发出光的波长最大 | |
| C. | 用这群氢原子所发的光照射逸出功为2.49eV的金属钠,则从金属钠表面所发出的光电子的最大初动能为11.11eV | |
| D. | 用这群氢原子所发的光照射逸出功为2.49eV的金属钠,则从金属钠表面所发出的光电子的最大初动能为9.60eV |
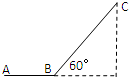 如图所示,某同学沿平直路面由A点出发前进了100m到达斜坡底端的B点,又沿倾角为60°的斜面前进了200m达到C点,求此同学的位移和路程.
如图所示,某同学沿平直路面由A点出发前进了100m到达斜坡底端的B点,又沿倾角为60°的斜面前进了200m达到C点,求此同学的位移和路程. 如图甲所示,单匝正方形闭合导线框abcd处在足够大的匀强磁场中,线框电阻为R,ab、ad的边长都为L;磁感应强度B的大小随时间变化的规律如图乙所示.
如图甲所示,单匝正方形闭合导线框abcd处在足够大的匀强磁场中,线框电阻为R,ab、ad的边长都为L;磁感应强度B的大小随时间变化的规律如图乙所示. 用多用表的欧姆档测量阻值约为几十kΩ的电阻Rx,以下给出的是可能的操作步骤,其中S为选择开关,P为欧姆档调零旋钮,把你认为正确的步骤前的字母按合理的顺序填写在下面的横线上.
用多用表的欧姆档测量阻值约为几十kΩ的电阻Rx,以下给出的是可能的操作步骤,其中S为选择开关,P为欧姆档调零旋钮,把你认为正确的步骤前的字母按合理的顺序填写在下面的横线上.