题目内容
(19分)“嫦娥三号”在月面成功软着陆,该过程可简化为:距月面15 km时,打开反推发动机减速,下降到距月面H=l00m.处时悬停,寻找合适落月点;然后继续下降,距月面h=4m时,速度再次减为零;此后关闭所有发动机,自由下落至月面。“嫦娥三号”质量为m(视为不变),月球质量是地球的k倍.月球半径是地球的n倍,地球半径为R、表面重力加速度为g;月球半径远大于H,不计月球自转的影响。以下结果均用题中所给符号表示。
(1)求月球表面的重力加速度大小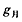 ;
;
(2)求“嫦娥三号”悬停时反推发动机的推力大小F,以及从悬停处到落至月面过程中所有发动机对“嫦峨三号”做的功W;
(3)取无穷远处为零势能点,月球引力范围内质量为m的物体具有的引力势能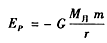 ,式中G为万有引力常量,
,式中G为万有引力常量, 为月球的质量,r为物体到月心的距离。若使“嫦娥三号”从月面脱离月球引力作用,忽略其它天体的影响,发射速度v0至少多大?(用k、n、g、R表示)
为月球的质量,r为物体到月心的距离。若使“嫦娥三号”从月面脱离月球引力作用,忽略其它天体的影响,发射速度v0至少多大?(用k、n、g、R表示)
(1)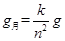 (2)
(2)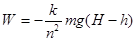 (3)
(3)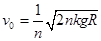
解析试题分析:(1)嫦娥三号在地球上,根据万有引力定律有: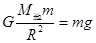
嫦娥三号在月球上,根据万有引力定律有: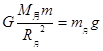 ,又
,又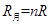 ,解得
,解得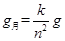
(2)嫦娥三号悬停时,由平衡条件可得 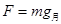 ,由上式可得:
,由上式可得: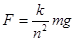
嫦娥三号由悬停到落至月面,由功能关系有: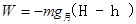 ,解得
,解得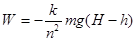
(3)嫦娥三号从月面到无穷远处过程中,由能量守恒定律,有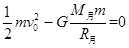 ,由上述式子联立可得:
,由上述式子联立可得: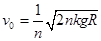
考点:万有引力定律的应用及能量守恒定律;

练习册系列答案
相关题目
某人造地球卫星在距地面高度为h的圆形轨道上绕地球做匀速圆周运动。已知地球质量为M,地球半径为R,卫星质量为m,引力常量为G。则卫星在圆形轨道上运行时
A.线速度大小 | B.线速度大小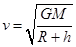 |
C.角速度大小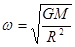 | D.角速度大小 |
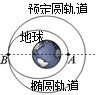
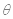 ,箱子做匀速直线运动.(引力常量为G)求:
,箱子做匀速直线运动.(引力常量为G)求: