题目内容
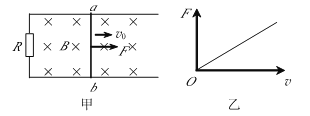
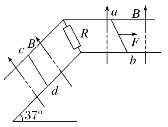
【题目】如图所示,两根相距L=1 m的足够长的光滑金属导轨,一组导轨水平,另一组导轨与水平面成37°角,拐角处连接一阻值R=1 Ω的电阻.质量均为m=2 kg的金属细杆ab、cd与导轨垂直接触形成闭合回路,导轨电阻不计,两杆的电阻均为R=1 Ω.整个装置处于磁感应强度大小B=1 T、方向垂直于导轨平面的匀强磁场中.当ab杆在平行于水平导轨的拉力作用下沿导轨向右匀速运动时,cd杆静止.g=10 m/s2,sin 37°=0.6,cos 37°=0.8,求:
(1)水平拉力的功率;
(2)现让cd杆静止,求撤去拉力后ab杆产生的焦耳热
【答案】(1)864 W (2)864 J
【解析】
(1)根据安培力公式与平衡条件求出电流,然后又E=BLv求出电动势,应用欧姆定律求出金属杆的速度,由平衡条件求出水平拉力,然后应用P=Fv求出拉力的功率.
(2)由能量守恒定律求出产生的热量,然后应用焦耳定律求出ab杆产生的焦耳热.
(1)cd杆静止,由平衡条件可得mgsin θ=BIL,
解得I=12 A
由闭合电路欧姆定律得2I=![]() ,得v=36 m/s
,得v=36 m/s
水平拉力F=2BIL=24 N,
水平拉力的功率P=Fv=864 W
(2)撤去外力后ab杆在安培力作用下做减速运动,安培力做负功,先将棒的动能转化为电能,再通过电流做功将电能转化为整个电路产生的焦耳热,即焦耳热等于杆的动能的减小量,有Q=ΔEk=![]() mv2=1296 J
mv2=1296 J
而Q=I′2·![]() R·t,
R·t,
ab杆产生的焦耳热Q′=I′2·R·t,
所以Q′=![]() Q=864 J.
Q=864 J.

练习册系列答案
相关题目