题目内容
【题目】如图所示,位于竖直平面内的圆周与水平面相切于M点,与竖直墙相切于点A,竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环轨道的圆心。已知在同一时刻,甲、乙两球分别从A、B两点由静止开始沿光滑倾斜直轨道运动到M点。丙球由C点自由下落到M点。则( )
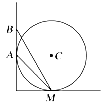
A. 甲球最先到达M点
B. 乙球最先到达M点
C. 丙球最先到达M点
D. 三个球同时到达M点
【答案】C
【解析】
对于三个小球,根据几何关系分别求出各个轨道的位移,根据牛顿第二定律求出加速度,再根据匀变速直线运动的位移时间公式求出运动的时间,从而比较出到达M点的先后顺序;
对于AM段,有几何关系得位移为x1=![]() R,由牛顿第二定律得加速度为:
R,由牛顿第二定律得加速度为:![]() ,根据x=
,根据x=![]() at2得:
at2得:![]() …①
…①
对于BM段,有几何关系得位移x2=2R,加速度为:a2=gsin60°=![]() g,根据x=
g,根据x=![]() at2得:
at2得:![]() …②
…②
对于CM段,位移x3=R,加速度a3=g,根据x=![]() at2得:
at2得:![]() …③
…③
比较①②③式可得:t2>t1>t3即丙球最先到达M点,乙球最后到达M点,故ABD错误,C正确;故选C。

练习册系列答案
相关题目