题目内容
9.在双缝干涉测光的波长的实验中,所用双缝间距d=2mm,双缝到屏的间距L=86.4cm,手轮的初始读数(第一条线)为ⅹ1=2.12mm,转动手轮,分划板中心刻线移动到第13条线,手轮读数ⅹ2=5.54mm,求通过滤光片后的波长.分析 通过第1条亮纹和第3条亮纹的距离求出相邻亮纹的距离,根据双缝干涉条纹的间距公式求出绿光的波长.
解答 解:相邻两条亮纹的距离为:
△x=$\frac{5.54-2.12}{13-1}$mm=0.285mm.
根据△x=$\frac{L}{d}$λ,解得:
λ=$\frac{△x•d}{L}$=$\frac{0.285×1{0}^{-3}×2×1{0}^{-3}}{0.864}$m=6.6×10-7m.
答:通过滤光片后的波长6.6×10-7m.
点评 解决本题的关键掌握双缝干涉条纹的间距公式△x=$\frac{L}{d}$λ.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
17.关于牛顿第一定律,下列说法中正确的是( )
| A. | 高速运动的物体不容易让它停下来,所以物体运动速度越大,惯性越大 | |
| B. | 牛顿第一定律也叫做惯性定律 | |
| C. | 牛顿第一定律只有物体不受力的作用时才成立 | |
| D. | 牛顿第一定律既提示了物体运动状态改变的原因是受到力的作用 |
4.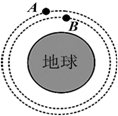 2010年12月18日,中国在西昌卫星发射中心用“长征三号甲”运载火箭,将第7颗北斗导航卫星成功送入太空预定轨道,继2010年10月成功发射“嫦娥二号”,我国又于2011年9月29日21时16分发射“天宫一号”目标飞行器,2011年下半年发射“神舟八号”飞船并将与“天宫一号”实现对接,届时将要有航天员在轨进行科研,这在我国航天史上具有划时代意义.“天宫一号”A和“神舟八号”B绕地球做匀速圆周运动的轨迹如图所示,虚线为各自的轨道.由此可知( )
2010年12月18日,中国在西昌卫星发射中心用“长征三号甲”运载火箭,将第7颗北斗导航卫星成功送入太空预定轨道,继2010年10月成功发射“嫦娥二号”,我国又于2011年9月29日21时16分发射“天宫一号”目标飞行器,2011年下半年发射“神舟八号”飞船并将与“天宫一号”实现对接,届时将要有航天员在轨进行科研,这在我国航天史上具有划时代意义.“天宫一号”A和“神舟八号”B绕地球做匀速圆周运动的轨迹如图所示,虚线为各自的轨道.由此可知( )
 2010年12月18日,中国在西昌卫星发射中心用“长征三号甲”运载火箭,将第7颗北斗导航卫星成功送入太空预定轨道,继2010年10月成功发射“嫦娥二号”,我国又于2011年9月29日21时16分发射“天宫一号”目标飞行器,2011年下半年发射“神舟八号”飞船并将与“天宫一号”实现对接,届时将要有航天员在轨进行科研,这在我国航天史上具有划时代意义.“天宫一号”A和“神舟八号”B绕地球做匀速圆周运动的轨迹如图所示,虚线为各自的轨道.由此可知( )
2010年12月18日,中国在西昌卫星发射中心用“长征三号甲”运载火箭,将第7颗北斗导航卫星成功送入太空预定轨道,继2010年10月成功发射“嫦娥二号”,我国又于2011年9月29日21时16分发射“天宫一号”目标飞行器,2011年下半年发射“神舟八号”飞船并将与“天宫一号”实现对接,届时将要有航天员在轨进行科研,这在我国航天史上具有划时代意义.“天宫一号”A和“神舟八号”B绕地球做匀速圆周运动的轨迹如图所示,虚线为各自的轨道.由此可知( )| A. | “天宫一号”的线速度大于“神舟八号”的线速度 | |
| B. | “天宫一号”的向心加速度大于“神舟八号”的向心加速度 | |
| C. | “天宫一号”的周期大于“神舟八号”的周期 | |
| D. | “神舟八号”通过一次点火加速后可能与“天宫一号”实现对接 |
14. 质量为2m的长木板静止地放在光滑的水平面上,如图a所示,质量为m的小铅块(可视为质点)以水平速度v0滑上木板左端,恰能滑至木板右端与木板相对静止,铅块运动中所受的摩擦力始终不变.现将木板分成长度与质量均相等的两段(1、2)后紧挨着仍放在此水平面上,让小铅块以相同的初速度由木板1的左端开始滑动,如图b所示,由下列判断中正确的是( )
质量为2m的长木板静止地放在光滑的水平面上,如图a所示,质量为m的小铅块(可视为质点)以水平速度v0滑上木板左端,恰能滑至木板右端与木板相对静止,铅块运动中所受的摩擦力始终不变.现将木板分成长度与质量均相等的两段(1、2)后紧挨着仍放在此水平面上,让小铅块以相同的初速度由木板1的左端开始滑动,如图b所示,由下列判断中正确的是( )
 质量为2m的长木板静止地放在光滑的水平面上,如图a所示,质量为m的小铅块(可视为质点)以水平速度v0滑上木板左端,恰能滑至木板右端与木板相对静止,铅块运动中所受的摩擦力始终不变.现将木板分成长度与质量均相等的两段(1、2)后紧挨着仍放在此水平面上,让小铅块以相同的初速度由木板1的左端开始滑动,如图b所示,由下列判断中正确的是( )
质量为2m的长木板静止地放在光滑的水平面上,如图a所示,质量为m的小铅块(可视为质点)以水平速度v0滑上木板左端,恰能滑至木板右端与木板相对静止,铅块运动中所受的摩擦力始终不变.现将木板分成长度与质量均相等的两段(1、2)后紧挨着仍放在此水平面上,让小铅块以相同的初速度由木板1的左端开始滑动,如图b所示,由下列判断中正确的是( )| A. | 小铅块滑到木板2的右端前就与之保持相对静止 | |
| B. | 小铅块仍滑到木板2的右端与之保持相对静止 | |
| C. | 小铅块滑过木板2的右端后飞离木板 | |
| D. | 上面的三种情况都有可能出现 |
1.如图是在同一条直线上运动的A、B两质点的位移图象,由图可知( )


| A. | t=0时,A在B前面 | |
| B. | B在t2秒末追上A并在此后跑在A的前面 | |
| C. | 在0-t1时间内B的运动速度比A大 | |
| D. | B在0~t1时间内速度比A小,t1秒后大于A的速度 |

 在距离地面2m处A点竖直上抛一个小球,上升到最高点B点,距离地面8m,返回地面的过程中在距离地面5m处C点被接住,整个过程用时2s (如图所示),以C点为坐标原点建立直线坐标系,竖直向上为正方向.求:
在距离地面2m处A点竖直上抛一个小球,上升到最高点B点,距离地面8m,返回地面的过程中在距离地面5m处C点被接住,整个过程用时2s (如图所示),以C点为坐标原点建立直线坐标系,竖直向上为正方向.求: