题目内容
如图所示,小车A的质量M=2kg,置于光滑水平面上,初速度v=14m/s.质量m=0.1kg,带电量q=+0.2C的物体B(可视为质点),轻放在小车A的右端.在A、B所在的空间存在着匀强磁场,方向垂直于纸面向里,磁感应强度B=0.5T,物体与小车之间有摩擦力的作用,设小车足够长,g取10m/s2,求:(1)B物体在小车上的最大速度;
(2)B物体在小车上时,小车A的最小速度;
(3)此过程中因摩擦而产生的内能是多少?
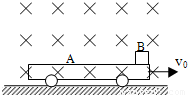
【答案】分析:当B物体对A物体压力为零时,A、B无摩擦力,B将做匀速直线运动,此时B的速度最大、A的速度最小.根据竖直方向上平衡求出B的速度,通过动量守恒定律求出A的速度.根据能量守恒定律求出系统增加的内能.
解答:解:(1)当洛仑兹力等于重力时,是B物体在小车上的最大速度,所以
qvBmB=mg
则vBm=10m/s
(2)当B在小车的上的速度最大时,A的速度最小,所以
由动量守恒有Mv=mvBm+MvA
解之得 vA=13.5m/s
(3)由能量守恒得
Q=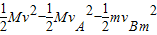
=8.75J
答:(1)B物体在小车上的最大速度为10m/s.
(2)B物体在小车上时,小车A的最小速度为13.5m/s.
(3)此过程中因摩擦而产生的内能是8.75J.
点评:解决本题的关键理清A、B的运动情况,确定何时A的速度最小,B的速度最大,结合动量守恒定律和能量守恒定律进行求解.
解答:解:(1)当洛仑兹力等于重力时,是B物体在小车上的最大速度,所以
qvBmB=mg
则vBm=10m/s
(2)当B在小车的上的速度最大时,A的速度最小,所以
由动量守恒有Mv=mvBm+MvA
解之得 vA=13.5m/s
(3)由能量守恒得
Q=
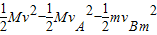
=8.75J
答:(1)B物体在小车上的最大速度为10m/s.
(2)B物体在小车上时,小车A的最小速度为13.5m/s.
(3)此过程中因摩擦而产生的内能是8.75J.
点评:解决本题的关键理清A、B的运动情况,确定何时A的速度最小,B的速度最大,结合动量守恒定律和能量守恒定律进行求解.

练习册系列答案
相关题目
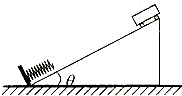 某节能运输系统的简化示意图如图所示.小车在倾斜直轨道顶端时,自动将货物装入车中,然后小车载着货物沿不光滑轨道无初速度下滑,到达轨道底端并压缩轻质弹簧.当弹簧被压缩到最短时,立即锁定小车,自动将货物卸下;卸完货物后随即解锁,小车被弹回,恰好能到达轨道顶端,此后周而复始的重复上述过程.己知小车与轨道间的动摩擦因数为μ,小车自身质量为m0,轨道倾角为θ,重力加速度为g,则下列说法正确的是( )
某节能运输系统的简化示意图如图所示.小车在倾斜直轨道顶端时,自动将货物装入车中,然后小车载着货物沿不光滑轨道无初速度下滑,到达轨道底端并压缩轻质弹簧.当弹簧被压缩到最短时,立即锁定小车,自动将货物卸下;卸完货物后随即解锁,小车被弹回,恰好能到达轨道顶端,此后周而复始的重复上述过程.己知小车与轨道间的动摩擦因数为μ,小车自身质量为m0,轨道倾角为θ,重力加速度为g,则下列说法正确的是( )| A、小车下滑过程中克服摩擦阻力做的功与小车上滑过程中克服摩擦阻力做的功相等 | ||
| B、在每一个运输周期中,货物减少的重力势能全部转化为摩擦热 | ||
| C、小车每次运载货物的质量可以不同 | ||
D、小车每次运载货物的质量是确定的,货物质量m=
|
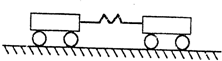 如图所示,在光滑的水平面上有两辆小车,中间夹一根压缩了的轻质弹簧,两手分别按住小车使它们静止,对两车及弹簧组成的系统,下列说法中正确的是( )
如图所示,在光滑的水平面上有两辆小车,中间夹一根压缩了的轻质弹簧,两手分别按住小车使它们静止,对两车及弹簧组成的系统,下列说法中正确的是( ) 如图所示,在光滑的水平面上有两辆小车,中间夹一根压缩了的轻质弹簧(与两车都不连接),两手分别按住小车使它们静止,对两车及弹簧组成的系统( )
如图所示,在光滑的水平面上有两辆小车,中间夹一根压缩了的轻质弹簧(与两车都不连接),两手分别按住小车使它们静止,对两车及弹簧组成的系统( )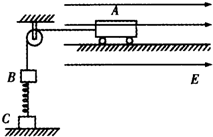 如图所示,小车A、小物块B由绕过轻质定滑轮的绝缘细线相连,小车A放在足够长的绝缘水平桌面上,B、C两小物块在竖直方向上通过劲度系数为k的轻质弹簧相连,C放在水平地面上,现用绝缘手柄控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与桌面平行.已知A、B、C的质量均为m,A与桌面间的动摩擦因数为0.2,重力加速度为g,细线与滑轮之间的摩擦不计,开始时,整个系统处于静止状态,A所在的空间有方向向右的匀强电场大小为E,现让A突然带电后,A向右运动至速度最大时,C恰好离开地面,在此过程中求:
如图所示,小车A、小物块B由绕过轻质定滑轮的绝缘细线相连,小车A放在足够长的绝缘水平桌面上,B、C两小物块在竖直方向上通过劲度系数为k的轻质弹簧相连,C放在水平地面上,现用绝缘手柄控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与桌面平行.已知A、B、C的质量均为m,A与桌面间的动摩擦因数为0.2,重力加速度为g,细线与滑轮之间的摩擦不计,开始时,整个系统处于静止状态,A所在的空间有方向向右的匀强电场大小为E,现让A突然带电后,A向右运动至速度最大时,C恰好离开地面,在此过程中求: