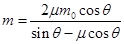题目内容
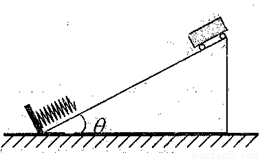
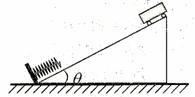
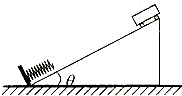某节能运输系统的简化示意图如图所示．小车在倾斜直轨道顶端时，自动将货物装入车中，然后小车载着货物沿不光滑轨道无初速度下滑，到达轨道底端并压缩轻质弹簧．当弹簧被压缩到最短时，立即锁定小车，自动将货物卸下；卸完货物后随即解锁，小车被弹回，恰好能到达轨道顶端，此后周而复始的重复上述过程．己知小车与轨道间的动摩擦因数为μ，小车自身质量为m0，轨道倾角为θ，重力加速度为g，则下列说法正确的是（ ）| A、小车下滑过程中克服摩擦阻力做的功与小车上滑过程中克服摩擦阻力做的功相等 | ||
| B、在每一个运输周期中，货物减少的重力势能全部转化为摩擦热 | ||
| C、小车每次运载货物的质量可以不同 | ||
D、小车每次运载货物的质量是确定的，货物质量m=
|
分析：对下滑过程和上滑过程分别进行受力分析，应用功的计算公式、能量守恒定律分析答题．
解答：解：A、小车克服摩擦力做功Wf=μmglcosθ，由于下滑过程与上滑过程小车的质量m不同，所以小车下滑过程中克服摩擦阻力做的功与小车上滑过程中克服摩擦阻力做的功不相等，故A错误；
B、在一个运输周期中，小车的机械能不变，货物的重力势能减少，在该过程中要克服摩擦力做功转化为内能，由能量守恒定律可知，货物减少的重力势能全部转化为摩擦热，故B正确；
C、小车每次下滑过程系统减小的重力势能等于弹簧的弹性势能和内能，要使小车回到最高点，必须保证每次弹簧的压缩量相同，故小车每次运载货物的质量必须是确定的，故C错误；
D、设每次运输货物的质量为m，由能量守恒定律得：mgs?sinθ=μ（m+m0）gs?cosθ+μm0gs?cosθ，解得：
m=
，故D正确；
故选：BD．
B、在一个运输周期中，小车的机械能不变，货物的重力势能减少，在该过程中要克服摩擦力做功转化为内能，由能量守恒定律可知，货物减少的重力势能全部转化为摩擦热，故B正确；
C、小车每次下滑过程系统减小的重力势能等于弹簧的弹性势能和内能，要使小车回到最高点，必须保证每次弹簧的压缩量相同，故小车每次运载货物的质量必须是确定的，故C错误；
D、设每次运输货物的质量为m，由能量守恒定律得：mgs?sinθ=μ（m+m0）gs?cosθ+μm0gs?cosθ，解得：
m=
| 2μm0cosθ |
| sinθ-μcosθ |
故选：BD．
点评：分析清楚小车的运动过程，应用功的计算公式、能量守恒定律即可正确解题．
练习册系列答案
相关题目
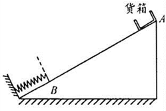
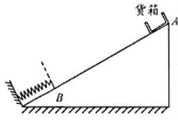如图为某节能运输系统的简化示意图．其工作原理为：货箱在轨道顶端A时，自动将货物装入货箱，然后货箱载着货物沿粗糙程度各处相同的轨道无初速度下滑，接着压缩弹簧，当弹簧被压缩至最短时，立即锁定并自动将货物卸下，卸完物后随即解锁，货箱恰好被弹回到A，此后重复上述过程．若弹簧为自由长度时右端对应的斜面位置是B，货箱可看作质点，则下列说法正确的是（ ）| A、货箱每次运载货物的质量相等 | B、锁定前瞬间货箱所受合外力等于解锁后瞬间货箱所受合外力 | C、小车上滑过程中克服摩擦阻力做的功小于小车下滑过程中克服摩擦阻力做的功 | D、小车与货物从顶端滑到最低点的过程中，减少的重力势能全转化为弹簧的弹性势能 |
，小车自身质量为
，轨道倾角为
，重力加速度为g，则下列说法正确的是
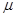，小车自身质量为
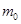，轨道倾角为
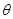，重力加速度为g，则下列说法正确的是
