题目内容
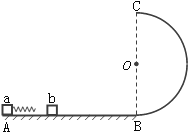
【题目】如图,水平光滑轨道AB与半径为R的竖直光滑半圆形轨道BC相切于B点。质量为2m和m的a、b两个小滑块(可视为质点)原来静止于水平轨道上,其中小滑块a与一轻弹簧相连。某一瞬间给小滑块a一冲量使其获得初速度向右冲向小滑块b,与b碰撞后弹簧不与b相粘连,且小滑块b在到达B点之前已经和弹簧分离,不计一切摩擦,小滑块b离开C点后落地点距离B点的距离为2R,重力加速度为g,求:
(1)小滑块b与弹簧分离时的速度大小vB;
(2)上述过程中a和b在碰撞过程中弹簧获得的最大弹性势能 Epmax;
(3)若刚开始给小滑块a的冲量为I=3m![]() ,求小滑块b滑块离开圆轨道的位置和圆心的连线与水平方向的夹角θ。(求出θ角的正弦函数值即可)。
,求小滑块b滑块离开圆轨道的位置和圆心的连线与水平方向的夹角θ。(求出θ角的正弦函数值即可)。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
解:(1)小滑块b脱离C点后,由平抛运动规律有:![]()
![]()
解得:![]()
小滑块b 恰好通过C点。
以B点为零势能点,小滑块b从B点到C点由机械能守恒定律有
![]()
则小滑块b与弹簧分离时的速度![]()
(2)小滑块b与弹簧分离过程满足动量和能量守恒: ![]()
![]()
解得:![]()
![]()
当弹簧压缩至最短时弹簧的弹性势能最大,由动量守恒定律和能量守恒定律有:
![]()
![]()
解得:![]()
(3)由动量定理有:![]()
解得: ![]()
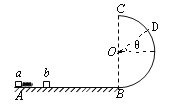
可知小滑块b不能通过C点,设小滑块b到达D点时离开,如图所示设倾角为![]() ,刚好离开有N=0,由牛顿第二定律有:
,刚好离开有N=0,由牛顿第二定律有:![]()
由动量守恒定律和能量守恒定律可知b脱离弹簧的速度为:![]()
从B到D由机械能守恒有:![]()
解得 ![]()

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目