题目内容
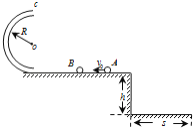
【题目】用细线把小球悬挂在墙壁上的钉子O上，小球绕悬点O在竖直平面内做圆周运动。小球质量为m，绳长为L，悬点距地面高度为H。小球运动至最低点时，绳恰被拉断，小球着地时水平位移为S，重力加速度为g，求：
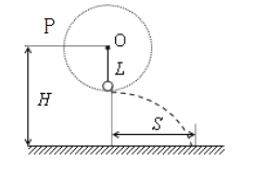
（1）细线刚被拉断时，小球抛出的速度多大？
（2）细线所能承受的最大拉力？
（3）如果绳子的长度L可变，将小球拉至P点（与O点在同一水平面），绳子刚好绷直，静止释放后到达最低时的速度为
，此时绳子刚好断（可用其它技术进行处理），小球水平飞出，试问：L与H的大小关系满足什么关系时，小球水平位移最大？最大位移是多少？
【答案】
；
；H
【解析】
（1）绳子烧断后，小球在水平方向做匀速运动即：
在竖直方向做自由落体运动即：
联立解得：
（2）小球运动到最低点时绳子刚好拉断设此时绳子的拉力为
，根据牛顿第二定律可知
解得：
（3）小球以速度
开始做平抛运动
在水平方向上：
在竖直方向上：
联立解得：
当
即
时水平位移有最大值，且最大值为：
练习册系列答案
相关题目
