Question

如下图所示，光滑水平面上某处固定着一个长度为0.5 m，高度为0.3 m的粗糙斜面，质量为0.1 kg的物块A以40 m／s的速度与静止在水平面的物块B相碰，碰后两物块粘在一起。已知物块B的质量为0.9 kg，两个物块与斜面间的动摩擦因数均为0.1，求物块滑上斜面后又回到水平面时的动能。(重力加速度g=10 m／s²，不计物块在平面和斜面连接处的能量损失)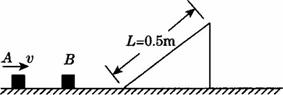

Answer 1

A、B两个物体碰撞，动量守恒：

m_Av=(m_A+m_B)v₁  解得：v₁=4 m／s  ①

两个物体结合后的动能：=(m_A+m_B)  ②

由①②得：=8J  ③

由动能定理可以求出物体在斜面末端动能：

-(m_A+m_B)gH-μ(m_A+m_B)gLcos θ=  ④

Leosθ=  ⑤

由④⑤得：=4.6J  ⑥

所以，物体飞离斜面末端，落回水平面。

-μ(m_A+m_B)gL cosθ=E_k-  ⑦

解得：E_k=-μ(m_A+m_B)gLcos θ=7.6 J  ⑧