题目内容
【题目】简谐运动是我们研究过的一种典型运动形式。
![]() 如图1所示,将两个劲度系数分别为
如图1所示,将两个劲度系数分别为![]() 和
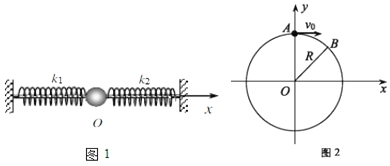
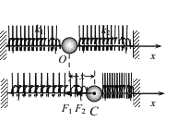
和![]() 的轻质弹簧套在光滑的水平杆上,弹簧的两端固定,中间接一质量为m的小球,此时两弹簧均处于原长。现将小球沿杆拉开一段距离后松开,小球以O为平衡位置往复运动,试证明,小球所做的运动是简谐运动。
的轻质弹簧套在光滑的水平杆上,弹簧的两端固定,中间接一质量为m的小球,此时两弹簧均处于原长。现将小球沿杆拉开一段距离后松开,小球以O为平衡位置往复运动,试证明,小球所做的运动是简谐运动。
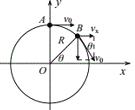
![]() 如图2所示,一质点以速度v0做半径为R的匀速圆周运动。试分析小球在x方向上的分运动是否为简谐运动。
如图2所示,一质点以速度v0做半径为R的匀速圆周运动。试分析小球在x方向上的分运动是否为简谐运动。
【答案】![]() 若小球向右偏离的位移为x,选取向右为正方向,由胡克定律可得,小球受到的合外力:
若小球向右偏离的位移为x,选取向右为正方向,由胡克定律可得,小球受到的合外力:![]() ,由于
,由于![]() 和
和![]() 都是常数,所以小球受到的合外力与位移成正比,小球做简谐振动。
都是常数,所以小球受到的合外力与位移成正比,小球做简谐振动。![]() 小球在x方向上的分运动符合简谐运动的特点。
小球在x方向上的分运动符合简谐运动的特点。
【解析】
![]() 若小球向右偏离的位移为x,选取向右为正方向,如图所示,由胡克定律可得,小球此时受到两个弹力F1和F2,方向沿x轴负方向,两个力的合力即小球受到的恢复力:F合=-(k1+k2)x,由于k1和k2都是常数,所以小球受到的合外力与位移成正比,方向相反,由此证明小球做简谐振动。
若小球向右偏离的位移为x,选取向右为正方向,如图所示,由胡克定律可得,小球此时受到两个弹力F1和F2,方向沿x轴负方向,两个力的合力即小球受到的恢复力:F合=-(k1+k2)x,由于k1和k2都是常数,所以小球受到的合外力与位移成正比,方向相反,由此证明小球做简谐振动。
![]() 质点从A运动到B,在B点将速度分解,如图所示:
质点从A运动到B,在B点将速度分解,如图所示:
A点速度v0沿x轴正方向,所以v0即为x方向经过平衡位置O点的速度
B点在x方向的投影为x,则![]() =
=![]()
B点加速度沿x方向的投影ax=-![]()
由牛顿第二定律可得:Fx=max=-m![]() =-m
=-m![]() x
x
小球以速度v0做半径为R的匀速圆周运动,其中m![]() 为常数,说明小球在x方向受到的合外力与位移成正比,方向相反,所以小球在x方向上的分运动符合简谐运动的特点。
为常数,说明小球在x方向受到的合外力与位移成正比,方向相反,所以小球在x方向上的分运动符合简谐运动的特点。
答案为:![]() 若小球向右偏离的位移为x,选取向右为正方向,由胡克定律可得,小球受到的合外力:
若小球向右偏离的位移为x,选取向右为正方向,由胡克定律可得,小球受到的合外力:![]() ,由于
,由于![]() 和
和![]() 都是常数,所以小球受到的合外力与位移成正比,小球做简谐振动。
都是常数,所以小球受到的合外力与位移成正比,小球做简谐振动。![]() 小球在x方向上的分运动符合简谐运动的特点。
小球在x方向上的分运动符合简谐运动的特点。

练习册系列答案
相关题目