题目内容
(1)已知地球质量为M,引力常量为G,地球自转周期为T.求同步卫星离地心的距离.
(2)已知地球半径为R, 地球自转周期为T,贴近地球运行的卫星的周期为T0.求同步卫星离地心的距离.
(3)已知地球半径为R,地面附近引力场强度约等于地面附近重力加速度g,地球自转周期为T.求同步卫星离地心的距离.
(2)已知地球半径为R, 地球自转周期为T,贴近地球运行的卫星的周期为T0.求同步卫星离地心的距离.
(3)已知地球半径为R,地面附近引力场强度约等于地面附近重力加速度g,地球自转周期为T.求同步卫星离地心的距离.
r=[GMT2/(4π2)]1/3 r=(T2/T02)1/3R r=[gR2T2/(4π2)] 1/3
试题分析:
(1)设同步卫星离地心的距离为r. 地球对同步卫星的万有
引力F产生向心加速度a:
而 F=GMm/r2 a=ω2r=4π2r/T2
所以 GMm/r2=4π2mr/T2
即 GMT2=4π2r3
于是 r=[GMT2/(4π2)]1/3 (4分)
(2)同步卫星的运行周期等于地球的自转周期T.设同步卫星离
地心的距离为r.由 GMm/r2=4π2mr/T2
可以得到 GMT2=4π2r3
类似地,贴近地球运行的卫星满足 GMT02=4π2R3
由以上两式可得 T2/T02=r3/R3 于是 r=(T2/T02)1/3R (4分)
(3)同步卫星的运行周期等于地球自转的周期T.设同步卫星离
地球的距离为r.则 GMm/r2=4π2mr/T2 即 r=[GMT2/(4π2)]1/3
又 g=F/m1=(GMm1/R2)/m1即 g=GM/R2
即 GM=gR2 可得r=[gR2T2/(4π2)] 1/3 (4分)
点评:万有引力充当向心力,然后结合牛顿第二定律列式求解

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目

 =
=
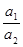 =
=


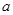 变为近月圆形轨道
变为近月圆形轨道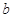 ,如图2所示在
,如图2所示在
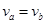
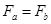
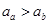
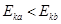
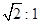 ,则这两颗卫星的运转半径之比为________,运转周期之比为________。
,则这两颗卫星的运转半径之比为________,运转周期之比为________。