题目内容
13.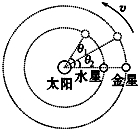 如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1,金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )
如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1,金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )| A. | 水星和金星的质量之比 | |
| B. | 水星和金星绕太阳运动的轨道半径之比 | |
| C. | 水星和金星绕太阳运动的周期之比 | |
| D. | 水星和金星绕太阳运动的向心加速度大小之比 |
分析 相同时间内水星转过的角度为θ1;金星转过的角度为θ2,可知道它们的角速度之比,绕同一中心天体做圆周运动,万有引力提供向心力:$\frac{GMm}{r^2}=m{ω^2}r$,可求出轨道半径比,以及向心加速度比,周期与角速度成反比.
解答 解:C、相同时间内水星转过的角度为θ1;金星转过的角度为θ2,可知它们的角速度之比为θ1:θ2.周期$T=\frac{2π}{ω}$,则周期比为θ2:θ1,故C正确;
A、水星和金星是环绕天体,无法求出质量,故不能得到它们的质量之比,故A错误;
B、万有引力提供向心力:$\frac{GMm}{r^2}=m{ω^2}r$,解得:$r=\root{3}{{\frac{GM}{ω^2}}}$.知道了角速度比,就可求出轨道半径之比,故B正确;
D、根据a=rω2,轨道半径之比、角速度之比都知道,很容易求出向心加速度之比,故D正确;
故选:BCD
点评 解决本题的关键掌握万有引力提供向心力:$\frac{GMm}{r^2}=m{ω^2}r$.以及知道要求某一天体的质量,要把该天体放在中心天体位置,放在环绕天体位置,被约去,求不出来

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
4.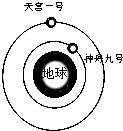 2012年6月,天宮一号与神舟九号载人交会对接任务获得圆满成功,假如神舟九号与天宮一号对接前所处的轨道如图所示,当它们处在图示的轨道时,下列说法正确的是( )
2012年6月,天宮一号与神舟九号载人交会对接任务获得圆满成功,假如神舟九号与天宮一号对接前所处的轨道如图所示,当它们处在图示的轨道时,下列说法正确的是( )
 2012年6月,天宮一号与神舟九号载人交会对接任务获得圆满成功,假如神舟九号与天宮一号对接前所处的轨道如图所示,当它们处在图示的轨道时,下列说法正确的是( )
2012年6月,天宮一号与神舟九号载人交会对接任务获得圆满成功,假如神舟九号与天宮一号对接前所处的轨道如图所示,当它们处在图示的轨道时,下列说法正确的是( )| A. | 神舟九号的运行速度比天宫号的大 | |
| B. | 神舟九号的运行的线速度比天宮一号的大 | |
| C. | 神舟九号的运行周期比天宮一号的大 | |
| D. | 神舟九号的加速度比天宫一号的大 |
8. 一带正电粒子仅在电场力作用下从A点经B、C运动到D点,其v-t图象如图所示,则下列说法中正确的是( )
一带正电粒子仅在电场力作用下从A点经B、C运动到D点,其v-t图象如图所示,则下列说法中正确的是( )
 一带正电粒子仅在电场力作用下从A点经B、C运动到D点,其v-t图象如图所示,则下列说法中正确的是( )
一带正电粒子仅在电场力作用下从A点经B、C运动到D点,其v-t图象如图所示,则下列说法中正确的是( )| A. | A处的电场强度一定小于B处的电场强度 | |
| B. | A处的电势一定小于在B处的电势 | |
| C. | CD间各点电场强度和电势都为零 | |
| D. | AB两点间的电势差等于CB两点间的电势差 |
5. 在绝缘光滑的水平面上x=-3L和 x=3L两处分别固定两个电荷QA、QB,两电荷连线之间的电势φ与位置x之间的关系图象,图中x=L点为图线的最低点,若在x=2L处由静止释放一个质量为m、带电荷量为+q的带电小球(可视为质点),下列有关说法正确的是( )
在绝缘光滑的水平面上x=-3L和 x=3L两处分别固定两个电荷QA、QB,两电荷连线之间的电势φ与位置x之间的关系图象,图中x=L点为图线的最低点,若在x=2L处由静止释放一个质量为m、带电荷量为+q的带电小球(可视为质点),下列有关说法正确的是( )
 在绝缘光滑的水平面上x=-3L和 x=3L两处分别固定两个电荷QA、QB,两电荷连线之间的电势φ与位置x之间的关系图象,图中x=L点为图线的最低点,若在x=2L处由静止释放一个质量为m、带电荷量为+q的带电小球(可视为质点),下列有关说法正确的是( )
在绝缘光滑的水平面上x=-3L和 x=3L两处分别固定两个电荷QA、QB,两电荷连线之间的电势φ与位置x之间的关系图象,图中x=L点为图线的最低点,若在x=2L处由静止释放一个质量为m、带电荷量为+q的带电小球(可视为质点),下列有关说法正确的是( )| A. | 小球在x=L处的速度最大 | B. | 小球可以到达x=-2L点处 | ||
| C. | 小球将以x=L点为中点做往复运动 | D. | QA、QB为同种电荷,且QA>QB |
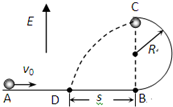 如图所示,竖直平面内有一半径为R的半圆形光滑绝缘轨道,其底端B与光滑绝缘水平轨道相切,整个系统处在竖直向上的匀强电场中,一质量为m,带电荷量为+q的小球以v0的初速度沿水平面向右运动,通过圆形轨道恰能到达圆形轨道的最高点C,从C点飞出后落在水平面上的D点,试求:
如图所示,竖直平面内有一半径为R的半圆形光滑绝缘轨道,其底端B与光滑绝缘水平轨道相切,整个系统处在竖直向上的匀强电场中,一质量为m,带电荷量为+q的小球以v0的初速度沿水平面向右运动,通过圆形轨道恰能到达圆形轨道的最高点C,从C点飞出后落在水平面上的D点,试求: 美国宇航局2015年7月24日0时(北京时间)宣布,可能发现了“另一个地球”-开普勒-452b,它距离地球1400光年.如果将开普勒-452b简化成如图所示的模型:MN为该星球的自转轴线,A、B是该星球表面上的两点(A在极地,B在赤道上);现在A、B两点各放置一质量为m的物体,用精密弹簧秤在A点称量物体,平衡时其示数为F,在B点称量物体,平衡时其示数为99.9%F,已知该星球的半径为R,试求:
美国宇航局2015年7月24日0时(北京时间)宣布,可能发现了“另一个地球”-开普勒-452b,它距离地球1400光年.如果将开普勒-452b简化成如图所示的模型:MN为该星球的自转轴线,A、B是该星球表面上的两点(A在极地,B在赤道上);现在A、B两点各放置一质量为m的物体,用精密弹簧秤在A点称量物体,平衡时其示数为F,在B点称量物体,平衡时其示数为99.9%F,已知该星球的半径为R,试求: