题目内容
18.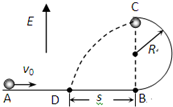 如图所示,竖直平面内有一半径为R的半圆形光滑绝缘轨道,其底端B与光滑绝缘水平轨道相切,整个系统处在竖直向上的匀强电场中,一质量为m,带电荷量为+q的小球以v0的初速度沿水平面向右运动,通过圆形轨道恰能到达圆形轨道的最高点C,从C点飞出后落在水平面上的D点,试求:
如图所示,竖直平面内有一半径为R的半圆形光滑绝缘轨道,其底端B与光滑绝缘水平轨道相切,整个系统处在竖直向上的匀强电场中,一质量为m,带电荷量为+q的小球以v0的初速度沿水平面向右运动,通过圆形轨道恰能到达圆形轨道的最高点C,从C点飞出后落在水平面上的D点,试求:(1)小球到达C点时的速度vC
(2)小球通过B点时,轨道对小球的支持力FN.
分析 (1)由动能定理可以求出小球到达C点的速度,小球恰能到达最高点C,说明在C点,轨道对小球没有作用力,重力与电场力的合力提供小球做圆周运动的向心力,由牛顿第二定律列方程,解方程组可以求出小球到达C时的速度.
(2)小球在圆形轨道上做圆周运动,由牛顿第二定律可以求出在B点小球受到的支持力,然后求出轨道受到的压力.
解答 解:(1)从B到C过程中,由动能定理得:
(qE-mg)×2R=$\frac{1}{2}$mvC2-$\frac{1}{2}$mv02,
小球恰能通过最高点,由牛顿第二定律得:mg-qE=m$\frac{{v}_{C}^{2}}{R}$,
解得:vC=$\frac{\sqrt{5}}{5}$v0
(2)小球在B点时,由牛顿第二定律得:
F+qE-mg=m$\frac{{v}_{0}^{2}}{R}$,
解得:F=$\frac{6m{v}_{0}^{2}}{5R}$,
由牛顿第三定律得,小球对轨道的压力F′=$\frac{6m{v}_{0}^{2}}{5R}$;
答:(1)小球到达C点时的速度为$\frac{\sqrt{5}}{5}$v0.
(2)小球通过B点时对轨道的压力为$\frac{6m{v}_{0}^{2}}{5R}$.
点评 要知道小球恰能到达最高点C的含义,熟练应用动能定律、牛顿第二定律的运动规律即可正确解题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
8.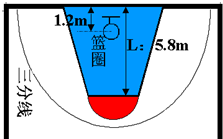 在一节篮球课中,某同学站在罚球线中央进行罚球表演(如图),关于篮球的位移和路程的说法正确的是( )
在一节篮球课中,某同学站在罚球线中央进行罚球表演(如图),关于篮球的位移和路程的说法正确的是( )
 在一节篮球课中,某同学站在罚球线中央进行罚球表演(如图),关于篮球的位移和路程的说法正确的是( )
在一节篮球课中,某同学站在罚球线中央进行罚球表演(如图),关于篮球的位移和路程的说法正确的是( )| A. | 篮球的位移为4.6m | |
| B. | 罚球点到篮圈的直线距离为篮球的路程 | |
| C. | 篮球的飞行路线的长度是篮球的位移 | |
| D. | 篮球的路程总比篮球的位移长 |
9. 如图所示,两块木块并排固定在水平面上,一子弹以速度v水平射入,若子弹在木块中做匀减速直线运动,穿过两木块时速度刚好减小到零,且穿过每块木块所用的时间相等,则两木块的厚度之比d1:d2为( )
如图所示,两块木块并排固定在水平面上,一子弹以速度v水平射入,若子弹在木块中做匀减速直线运动,穿过两木块时速度刚好减小到零,且穿过每块木块所用的时间相等,则两木块的厚度之比d1:d2为( )
 如图所示,两块木块并排固定在水平面上,一子弹以速度v水平射入,若子弹在木块中做匀减速直线运动,穿过两木块时速度刚好减小到零,且穿过每块木块所用的时间相等,则两木块的厚度之比d1:d2为( )
如图所示,两块木块并排固定在水平面上,一子弹以速度v水平射入,若子弹在木块中做匀减速直线运动,穿过两木块时速度刚好减小到零,且穿过每块木块所用的时间相等,则两木块的厚度之比d1:d2为( )| A. | 1:3 | B. | 1:4 | C. | 3:1 | D. | 4:1 |
6.如图所示,杯子落到水平桌面时,则下列说法正确的是( )
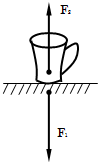

| A. | 力F1就是杯子的重力 | B. | 力F1和力F2是一对平衡力 | ||
| C. | 力F1是由杯子发生形变产生的 | D. | 力F1的大小大于力F2的大小 |
13.下列说法正确的是( )
| A. | 超高压带电作业的工人所穿衣服的织物中掺入金属丝是为了增加衣服的导电性 | |
| B. | 避雷针能够避免建筑物被雷击的原因是云层中带的电荷被避雷针通过导线导入大地 | |
| C. | 静电除尘的原理是烟雾颗粒被强电场粉碎成更小的颗粒,排到大气中人眼看不到 | |
| D. | 用金属箔做成一个不带电的圆环.用绝缘材料做的笔套与头发摩擦后,慢慢靠近圆环,距离约为0.5cm时圆环被吸引到笔套上,笔套碰到圆环后,笔套所带的电荷立刻被全部中和 |
10.图中R1=4Ω,R2=9Ω,R3=18Ω.通电后( )
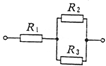

| A. | 经R1和R3的电流之比I1:I3=1:3 | |
| B. | R1两端的电压和R3两端的电压之比U1:U3=4:9 | |
| C. | 三个电阻消耗的电功率之比P1:P2:P3=2:1:2 | |
| D. | 三个电阻消耗的电功率之比P1:P2:P3=2:2:1 |
7. “嫦娥”三号月球探测器“玉兔”号月球车立于着陆器的顶部.着陆器与月球车分离时,“玉兔”号沿着着陆器与月面之间搭起一架斜梯运动,最后顺利驶抵月球表面,如图所示.假设“玉兔”号月球车在斜梯上匀速移动,则在此过程中( )
“嫦娥”三号月球探测器“玉兔”号月球车立于着陆器的顶部.着陆器与月球车分离时,“玉兔”号沿着着陆器与月面之间搭起一架斜梯运动,最后顺利驶抵月球表面,如图所示.假设“玉兔”号月球车在斜梯上匀速移动,则在此过程中( )
 “嫦娥”三号月球探测器“玉兔”号月球车立于着陆器的顶部.着陆器与月球车分离时,“玉兔”号沿着着陆器与月面之间搭起一架斜梯运动,最后顺利驶抵月球表面,如图所示.假设“玉兔”号月球车在斜梯上匀速移动,则在此过程中( )
“嫦娥”三号月球探测器“玉兔”号月球车立于着陆器的顶部.着陆器与月球车分离时,“玉兔”号沿着着陆器与月面之间搭起一架斜梯运动,最后顺利驶抵月球表面,如图所示.假设“玉兔”号月球车在斜梯上匀速移动,则在此过程中( )| A. | 月球车在斜梯上没有受到摩擦力的作用 | |
| B. | 着陆器没有受到月球表面的摩擦力作用 | |
| C. | 着陆器一定受到月球表面的摩擦力作用 | |
| D. | 月球车在月球上受到的重力与在地球上的重力相等 |
13.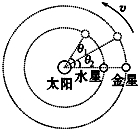 如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1,金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )
如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1,金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )
 如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1,金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )
如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1,金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )| A. | 水星和金星的质量之比 | |
| B. | 水星和金星绕太阳运动的轨道半径之比 | |
| C. | 水星和金星绕太阳运动的周期之比 | |
| D. | 水星和金星绕太阳运动的向心加速度大小之比 |
 如图所示,质量为m1的长木板A放置在水平地面上,质量为m2的木块B放在长木板A上,木块B与长木板A之间的动摩擦因数为μ1,长木板A与水平地面之间的动摩擦因数为μ2.现用大小为F的向右水平力拉木块B,使其沿着A向右运动,而A仍静止不动.
如图所示,质量为m1的长木板A放置在水平地面上,质量为m2的木块B放在长木板A上,木块B与长木板A之间的动摩擦因数为μ1,长木板A与水平地面之间的动摩擦因数为μ2.现用大小为F的向右水平力拉木块B,使其沿着A向右运动,而A仍静止不动.