题目内容
如图(甲)所示，两水平放置的平行金属板C、D相距很近，上面分别开有小孔O和
，水平放置的平行金属导轨P、Q与金属板C、D接触良好，且导轨垂直放在磁感强度为B1＝10 T的匀强磁场中，导轨间距L＝0.50 m，金属棒AB紧贴着导轨沿平行导轨方向在磁场中做往复运动，其速度图象如图(乙)，若规定向右运动速度方向为正方向．从t＝0时刻开始，由C板小孔O处连续不断地以垂直于C板方向飘入质量为m＝3.2×10－21 kg、电量q＝1.6×10－19 C的带正电的粒子(设飘入速度很小，可视为零)．在D板外侧有以MN为边界的匀强磁场B2＝10 T，MN与D相距d＝10 cm，B1和B2方向如图所示(粒子重力及其相互作用不计)，求
(1)0到4.0 s内哪些时刻从O处飘入的粒子能穿过电场并飞出磁场边界MN？
(2)粒子从边界MN射出来的位置之间最大的距离为多少？
答案：
解析：
解析：
|
(1)只有当CD板间的电场力方向向上即AB棒向右运动时，粒子才可能从O运动到 设CD间的电压为U，则 解①②得U＝25 V，又U＝ε＝B1Lv 解得v＝5 m/s． 所以根据(乙)图可以推断在0.25 s＜t＜1.75 s内，粒子能穿过CD间的电场． (2)当AB棒速度最大，即 此时带电粒子经加速后速度为v，由动能定理有： 解得：v＝100 m/s此时带电粒子的轨道半径为 粒子从边界MN射出来的位置间最大距离为S＝d－x＝7.3 cm |
，而粒子要飞出磁场边界MN最小速度v0必须满足：
①
②
＝20 m/s时产生感应电动势为：
＝B1L
出射点与
的水平距离为：
练习册系列答案
名校课堂系列答案
相关题目
（1）如图（1）所示，是氢原子四个能级的示意图．当氢原子从n=4的能级跃迁到n=3的能级时，辐射出光子a．当氢原子从n=3的能级跃迁到n=2的能级时，辐射出光子b．则以下判断正确的是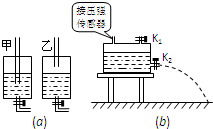
如图（a）所示，两个相同的盛水容器，密闭时装有相同水位的水．现在它们顶部各插有一根两端开口的玻璃管，甲容器中的玻璃管下端插入水中，乙容器中的玻璃管下端在水面上方．若打开容器底部的阀门，两个容器中均有水流出，在开始的一段时间内，水流出的速度不变的是
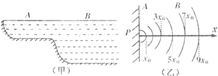浅水处水波的速度跟水的深度有关，其关系式为
