题目内容
 (1)如图(1)所示,是氢原子四个能级的示意图.当氢原子从n=4的能级跃迁到n=3的能级时,辐射出光子a.当氢原子从n=3的能级跃迁到n=2的能级时,辐射出光子b.则以下判断正确的是
(1)如图(1)所示,是氢原子四个能级的示意图.当氢原子从n=4的能级跃迁到n=3的能级时,辐射出光子a.当氢原子从n=3的能级跃迁到n=2的能级时,辐射出光子b.则以下判断正确的是C
C
A.光子a的能量大于光子b的能量
B.光子a的频率大于光子b的频率
C.光子a的波长大于光子b的波长
D.在真空中光子a的传播速度大于光子b的传播速度
(2)如图(2)所示,两只质量均为120kg的小船静止在水面上,相距10m,并用钢绳连接.一个质量为60kg的人在甲船头以恒力F拉绳,不计水的阻力,求:
(a)当两船相遇时,两船各行进了多少米?
(b)当两船相遇不相碰的瞬间,为了避免碰撞,人从甲船跳向乙船需要对地的最小水平速度为6m/s,计算原来人拉绳的恒力F.
分析:(1)根据玻尔理论判断光子a的能量与光子b的能量的大小.根据光子的能量E=hγ=h
判断光子的频率和波长的大小.所有光子在真空中传播速度相同.
(2)(a)用位移表示甲乙船的速度,根据动量守恒定律得出两船的位移关系,由两船位移之和等于10m,求出两船行进的距离.(b)由于两船原来都处于静止状态,总动量为零,为了避免碰撞,人跳到乙船后系统至少都要静止.根据动量守恒求出人在起跳前瞬间甲船和人的速度,根据动能定理求出原来人拉绳的恒力F.
| c |
| λ |
(2)(a)用位移表示甲乙船的速度,根据动量守恒定律得出两船的位移关系,由两船位移之和等于10m,求出两船行进的距离.(b)由于两船原来都处于静止状态,总动量为零,为了避免碰撞,人跳到乙船后系统至少都要静止.根据动量守恒求出人在起跳前瞬间甲船和人的速度,根据动能定理求出原来人拉绳的恒力F.
解答:解:
(1)A、根据玻尔理论得知,光子a的能量Ea=E4-E3=-0.85eV-(-1.51eV)=0.66eV,光子a的能量Eb=E3-E2=-1.51eV-(-3.4eV)=1.89eV.所以光子a的能量小于光子b的能量.故A错误.
B、根据光子的能量E=hγ得知,光子的能量与频率成正比,所以光子a的频率小于光子b的频率.故B错误.
C、光子的能量E=h
,光子的能量与波长成反比,所以光子a的波长大于光子b的波长.故C正确.
D、所有光子在真空中传播速度相同.故选D错误.
故选C
(2)(a)由动量守恒定律,得(m甲+m人)v甲-m乙v乙=0,
得到(m甲+m人)
=m乙
,
又s甲+s乙=10m得,
解得s甲=4m,s乙=6m
(b)为了避免碰撞,人跳到乙船后系统至少要静止.设人在起跳前瞬间甲船和人的速度为v1,乙船速度v2,
对甲船和人组成的系统由动量守恒得,(m甲+m人)v1=m人v人
得v1=2m/s
由动能定理得,Fs甲=
(m甲+m人)
,
解得F=90N.
故答案为:
(1)C
(2)(a)当两船相遇时,甲船行进4m,乙船行进6m;(b)原来人拉绳的恒力F=90N.
(1)A、根据玻尔理论得知,光子a的能量Ea=E4-E3=-0.85eV-(-1.51eV)=0.66eV,光子a的能量Eb=E3-E2=-1.51eV-(-3.4eV)=1.89eV.所以光子a的能量小于光子b的能量.故A错误.
B、根据光子的能量E=hγ得知,光子的能量与频率成正比,所以光子a的频率小于光子b的频率.故B错误.
C、光子的能量E=h
| c |
| λ |
D、所有光子在真空中传播速度相同.故选D错误.
故选C
(2)(a)由动量守恒定律,得(m甲+m人)v甲-m乙v乙=0,
得到(m甲+m人)
| s甲 |
| t |
| s乙 |
| t |
又s甲+s乙=10m得,
解得s甲=4m,s乙=6m
(b)为了避免碰撞,人跳到乙船后系统至少要静止.设人在起跳前瞬间甲船和人的速度为v1,乙船速度v2,
对甲船和人组成的系统由动量守恒得,(m甲+m人)v1=m人v人
得v1=2m/s
由动能定理得,Fs甲=
| 1 |
| 2 |
| v | 2 1 |
解得F=90N.
故答案为:
(1)C
(2)(a)当两船相遇时,甲船行进4m,乙船行进6m;(b)原来人拉绳的恒力F=90N.
点评:氢原子跃迁时遵守玻尔理论,光子的能量hγ=Em-En(m>n).第(2)题人拉船时,系统的动量守恒.基础题.

练习册系列答案
相关题目
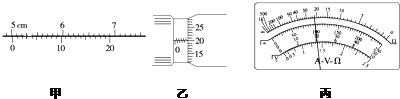
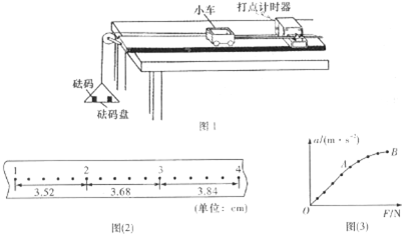
 (1)如图(1)所示,在验证动量守恒的实验中:
(1)如图(1)所示,在验证动量守恒的实验中:

