题目内容
13. 如图所示,两个半径分别为r1和r2的球,质量均匀分布,分别为m1和m2,两球之间的距离为r,则两球间的万有引力大小为( )
如图所示,两个半径分别为r1和r2的球,质量均匀分布,分别为m1和m2,两球之间的距离为r,则两球间的万有引力大小为( )| A. | G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$ | B. | G$\frac{{m}_{1}{m}_{2}}{(r+{r}_{1})^{2}}$ | ||
| C. | G$\frac{{m}_{1}{m}_{2}}{(r+{r}_{2})^{2}}$ | D. | G$\frac{{m}_{1}{m}_{2}}{(r+{r}_{1}+{r}_{2})^{2}}$ |
分析 应用万有引力公式可以求出两球间的万有引力,要注意r为两球心间的距离.
解答 解:两球间的万有引力:F=G$\frac{{m}_{1}{m}_{2}}{({r}_{1}+r+{r}_{2})^{2}}$;
故选:D.
点评 本题考查了万有引力定律的应用,考查了求两球间的万有引力,掌握理解万有引力公式即可解题,本题是一道基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
3.如图所示为同一实验室中两个单摆的振动图象,从图中可知,两摆的( )
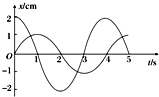

| A. | 摆长相等 | B. | 振幅相等 | ||
| C. | 摆球质量相等 | D. | 摆球同时改变速度方向 |
4. 如图所示,小球从光滑圆弧曲面上的A处由静止下滑,恰好能通过半径为r的光滑圆形轨道的最高点C,已知重力加速度为g,则( )
如图所示,小球从光滑圆弧曲面上的A处由静止下滑,恰好能通过半径为r的光滑圆形轨道的最高点C,已知重力加速度为g,则( )
 如图所示,小球从光滑圆弧曲面上的A处由静止下滑,恰好能通过半径为r的光滑圆形轨道的最高点C,已知重力加速度为g,则( )
如图所示,小球从光滑圆弧曲面上的A处由静止下滑,恰好能通过半径为r的光滑圆形轨道的最高点C,已知重力加速度为g,则( )| A. | 小球经过最高点C的速度为$\sqrt{gr}$ | |
| B. | 小球经过最高点时受到的向心力为0 | |
| C. | A点相对于B点的高度h=$\frac{5}{2}$r | |
| D. | 小球经过圆心轨道的最低点B时的加速度可能小于g |
8.人造卫星在地面附近绕地球做匀速圆周运动所必须具有的速度,称为第一宇宙速度.第一宇宙速度大小是( )
| A. | 11.2km/s | B. | 7.9km/s | C. | 16.7km/s | D. | 光速 |
2.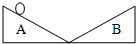 如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )
如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )
 如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )
如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )| A. | 高度 | B. | 动能 | C. | 势能 | D. | 能量 |
3.NBA篮球赛非常精彩,吸引了众多观众.2012-2013赛季总决赛第六场中,雷阿伦在终场前5.2s的时候,把球投出且准确命中,把比赛拖入加时从而让热火获得比赛的胜利.如果雷阿伦投篮过程中对篮球做功为W,出手高度为h1,篮筐距地面高度为h2,篮球的质量为m,空气阻力不计,则篮球进筐时的动能为( )
| A. | W+mgh1-mgh2 | B. | W+mgh2-mgh1 | C. | mgh1+mgh2-W | D. | mgh2-mgh1-W |
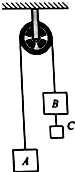 如图所示,三个物体A、B、C跨过定滑轮相连.已知物体A、B的质量相等均为M,物体C的质量为m,轻绳与轻滑轮间的摩擦不计,绳子不可伸长,如果m=$\frac{2}{3}$M,M为已知量,重力加速度为g,求:
如图所示,三个物体A、B、C跨过定滑轮相连.已知物体A、B的质量相等均为M,物体C的质量为m,轻绳与轻滑轮间的摩擦不计,绳子不可伸长,如果m=$\frac{2}{3}$M,M为已知量,重力加速度为g,求: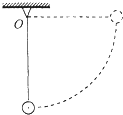 一个质量为m的小球,系在一根长度为1米的轻绳一端.将绳拉至水平位置后释放,求小球摆至最低点时速度为多少.
一个质量为m的小球,系在一根长度为1米的轻绳一端.将绳拉至水平位置后释放,求小球摆至最低点时速度为多少.