题目内容

18．一个质量为m的小球，系在一根长度为1米的轻绳一端．将绳拉至水平位置后释放，求小球摆至最低点时速度为多少．

分析 对小球运用动能定理，抓住只有重力做功，求出小球摆至最低点的速度大小．

解答 解：根据动能定理得，mgL=$\frac{1}{2}m{v}^{2}$得，
v=$\sqrt{2gL}=\sqrt{2×10×1}m/s=2\sqrt{5}m/s$．
答：小球摆至最低点的速度大小为$2\sqrt{5}m/s$．

点评 解决本题的关键知道小球在运动的过程中只有重力做功，结合动能定理进行求解，也可以根据机械能守恒定律进行求解，基础题．

练习册系列答案
相关题目
8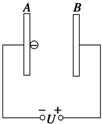．如图所示，在A板附近有一电子由静止开始向B板运动，则关于电子到达B板时的速率，下列解释正确的是（　　）
A．两板间距越大，加速的时间就越长，则获得的速率越大
B．两板间距越小，加速的时间就越长，则获得的速率不变
C．两板间距越大，加速的时间就越长，则获得的速率不变
D．两板间距越小，加速的时间越短，则获得的速率越小
9．如图甲所示的变压器电路中，理想变压器原、副线圈匝数之比为2：1，a、b输入端输入的电流如图乙所示，原、副线圈电路中电阻R1=R2=10Ω，下列说法正确的是（　　）
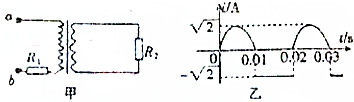
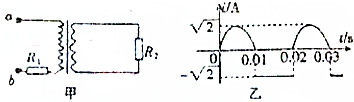
A．流经R1的电流为$\frac{\sqrt{6}}{2}$AB．R2两端的电压为10$\sqrt{5}$V
C．原线圈的输入电压有效值为40VD．a、b端输入电压有效值为（20$\sqrt{2}$+5$\sqrt{6}$）V
6．关于匀速圆周运动的线速度，下列说法中正确的是（　　）
A．大小和方向都保持不变B．大小和方向都时刻改变
C．大小不变，方向时刻改变D．大小时刻改变，方向不变
13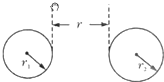．如图所示，两个半径分别为r1和r2的球，质量均匀分布，分别为m1和m2，两球之间的距离为r，则两球间的万有引力大小为（　　）
A．G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$B．G$\frac{{m}_{1}{m}_{2}}{（r+{r}_{1}）^{2}}$
C．G$\frac{{m}_{1}{m}_{2}}{（r+{r}_{2}）^{2}}$D．G$\frac{{m}_{1}{m}_{2}}{（r+{r}_{1}+{r}_{2}）^{2}}$
3．如图所示，电池的电动势为E，内阻为r，当滑动变阻器的滑动片P由a向b滑动的过程中，电流表、电压表的示数变化情况（　　）
A．电流表一直减小，电压表一直增大
B．电流表一直增大，电压表一直减小
C．电流表先减小后增大，电压表先增大后减小
D．电流表先增大后减小电压表先减小后增大
10．如图所示，在空旷地带研究飞镖在空气中的运动情况，下列说法正确的是（　　）
A．飞镖在空中的指向就是它做曲线运动的速度的方向
B．飞镖在空中做的是匀变速曲线运动
C．飞镖在空中运动的过程中机械能守恒
D．离地面的高度一定时，无论怎样改变飞镖的投射角，它落至地面的速度大小保持不变
7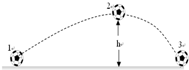．如图，质量为m的足球在地面1的位置被踢出后落到地面3的位置，在空中达到的最高点2的高度为h，则以下说法正确的是（　　）
A．从1到3，足球重力做功为2mgh
B．从2到3，足球重力做功为mgh，所以重力势能变化为mgh
C．从1到2，足球克服重力做功为mgh
D．从1到3，足球先做负功，后做正功，所以重力势能一直不变
8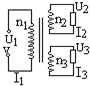．如图所示，理想变压器的原线圈匝数为n1，副线圈匝数分别为n2和n3，原、副 线圈电压分别为U1、U2、U3，电流分别为I1、I2、I3，两个副线圈所连电阻的阻值未知，则下面的结论中正确的是（　　）
A．U1：U2=n1：n2，U2：U3=n2：n3B．n1I1=n2I2+n3I3
C．I1：I2=n2：n1；I1：I3=n3：n1D．I1U1=I2U2+I3U3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网