题目内容
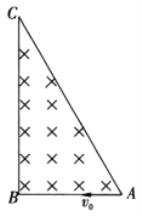
【题目】如图所示，直角三角形的AB边长为L，∠C为30°，三角形所围区域内存在着方向垂直纸面向里的匀强磁场。一质量为m、电荷量为q的带负电粒子(不计重力)从A点沿AB方向以速度v0射入磁场，要使粒子不从BC边穿出磁场，则下列说法正确的是
A. 磁感应强度的最小值为B=
B. 磁感应强度的最小值为B=
C. 粒子在磁场中运动的最长时间为t=
D. 粒子在磁场中运动的最长时间为t=
【答案】C
【解析】
粒子在磁场中做圆周运动，根据题意作出粒子临界运动轨迹，求出粒子临界轨道半径，应用牛顿第二定律求出磁感应强度的最小值；根据粒子在磁场中转过的最大圆心角求出粒子在磁场中运动的最长时间.
A、B、粒子恰好不从BC射出时运动轨迹如图所示：
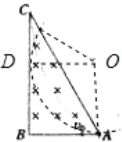
图中四边形ABDO是正方形，故圆周的半径为：r=L，
粒子在磁场中做圆周运动，由牛顿第二定律得：
，解得：
，粒子不从BC边射出：
，故A、B错误；
C、D、粒子从AC边射出磁场时在磁场中转过的圆心角最大为：120°，粒子在磁场中运动时间最长，粒子在磁场中的最长运动时间：
，故C正确，D错误；
故选C.
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
