题目内容
物块从最低点D以v0=4米/秒的速度滑上光滑的斜面,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到B的时间.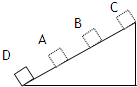

物块作匀减速直线运动.设A点速度为vA、B点速度vB,加速度为a,斜面长为S.
A到B:vB2-vA2=2asAB …(1)
vA=2vB …(2)
B到C:0=vB+at0 …..(3)
解(1)(2)(3)得:vB=1m/s a=-2m/s2
D到C:0-v02=2aS …(4)
S=4m
从D运动到B的时间:
D到B:vB=v0+at1 t1=1.5s
D到C再回到B:由于B到C和C到B的运动是对称的,所以运动的时间相等.
所以D到C再回到B的时间t2=t1+2t0=1.5+2×0.5=2.5s.
A到B:vB2-vA2=2asAB …(1)
vA=2vB …(2)
B到C:0=vB+at0 …..(3)
解(1)(2)(3)得:vB=1m/s a=-2m/s2
D到C:0-v02=2aS …(4)
S=4m
从D运动到B的时间:
D到B:vB=v0+at1 t1=1.5s
D到C再回到B:由于B到C和C到B的运动是对称的,所以运动的时间相等.
所以D到C再回到B的时间t2=t1+2t0=1.5+2×0.5=2.5s.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
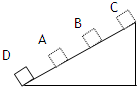 物块从最低点D以v0=4米/秒的速度滑上光滑的斜面,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到B的时间.
物块从最低点D以v0=4米/秒的速度滑上光滑的斜面,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到B的时间.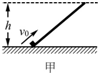 如图甲所示,小物块从斜面底端以初速度v0沿光滑斜面上滑,所能到达的最大高度距底端为h.下图为四个固定在竖直平面内的光滑圆轨道,O1、O2、O3和O4分别是它们的圆心.小物块仍以初速度v0从轨道最低点上滑,则小物块能上升到距水平地面高h处的是( )
如图甲所示,小物块从斜面底端以初速度v0沿光滑斜面上滑,所能到达的最大高度距底端为h.下图为四个固定在竖直平面内的光滑圆轨道,O1、O2、O3和O4分别是它们的圆心.小物块仍以初速度v0从轨道最低点上滑,则小物块能上升到距水平地面高h处的是( )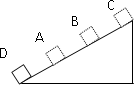
 物块从最低点D以v0=4米/秒的速度滑上光滑的斜面,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到B的时间.
物块从最低点D以v0=4米/秒的速度滑上光滑的斜面,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到B的时间.