题目内容

3．如图所示O1轴上有两个转动轮，大轮半径为2r，小轮的半径为r，轮O2的半径为 r，对于轮缘上的A、B、C三点，则：
ωA：ωB：ωC=1：1：2，
VA：VB：VC=2：1：2．

分析 对于A与C，由于皮带不打滑，线速度大小相等．对于B与A绕同一转轴转动，角速度相等，由v=ωr研究A与C的角速度关系，再根据a=ω2r求出向心加速度之比．

解答 解：对于A与B，绕同一转轴转动，角速度相等，即ωA=ωB．由v=ωr和R1：R2=2：1，所以：vA：vB=R1：R2=2：1
对于A与C，由于皮带不打滑，线速度大小相等，即vA=vC．由v=ωr得ωA：ωC=rC：rA=1：2．
由以上的分析，则ωA：ωB：ωC=1：1：2，vA：vB：vC=2：1：2
故答案为：1：1：2；2：1：2

点评 本题运用比例法解决物理问题的能力，关键抓住相等的量：对于不打滑皮带传动的两个轮子边缘上各点的线速度大小相等；同一轮上各点的角速度相同．

练习册系列答案
相关题目
6．如图所示，50个大小相同，质量为m的小物块，在平行于斜面向上的恒力作用下一起沿斜面向上运动，已知斜面足够长，倾角为30°，各物块与斜面的动摩擦因数相同，重力加速度为g，则第3个小物块对第2个小物块的作用力大小为0.96F．
14．从某点先后由静止释放金属小球A和B，不计空气阻力．若以B球为参照物，A球的运动是（　　）
A．匀加速直线运动B．匀速直线运动C．静止D．变加速直线运动
11．在5m高的地方，以6m/s初速度水平抛出一个质量为10kg的物体，求物体落地的速度大小是多少？（不计空气阻力，g=10m/s2）
18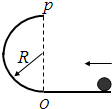．如图所示，一个质量为m的小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P，然后落回水平面．不计一切阻力．下列中说法正确的是（　　）
A．小球运动到半圆弧最高点P时向心力为零
B．小球落到地面前的瞬时其动能为$\frac{5mgR}{2}$
C．小球落地点离p点的水平距离为2$\sqrt{2}$R
D．若将半圆弧轨道上部的圆弧截去，其他条件不变，则小球能达到的最大高度比P点高0.5R
8．了解物理规律的发现过程，学会像科学家那样观察和思考，往往比掌握知识本身更重要．以下符合事实的是（　　）
A．伽利略通过“理想实验”得出“力是维持物体运动的原因”
B．楞次发现了电流的磁效应，拉开了研究电与磁相互关系的序幕
C．法拉第发现了通电导线的周围存在磁场
D．胡克认为只有在一定的条件下，弹簧的弹力才与弹簧的形变量成正比
15．一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动．用下面的方法测量它匀速转动时的角速度．实验器材：电磁打点计时器、米尺、纸带、复写纸片．
实验步骤：
①如图1所示，将电磁打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔后，固定在待测圆盘的侧面上，使得圆盘转动时，纸带可以卷在圆盘侧面上．
②启动控制装置使圆盘转动，同时接通电源，打点计时器开始打点．
③经过一段时间，停止转动和打点，取下纸带，进行测量．
（1）由已知量和测得量表示的角速度的表达式为ω=$\frac{L}{nTr}$，式中各量的意义是：式中T为电磁打点计时器打点的周期，r为圆盘的半径，L是用米尺测量的纸带上选定的两点间的长度，n为选定的两点间的打点周期数．
（2）某次实验测得圆盘半径r=5.50×10-2 m，得到的纸带的一段如图2所示，求得角速度为6.7rad/s．（保留两位有效数字）
12．矿井里的升降机从静止开始作匀加速直线运动，上升3s速度达到3m/s，然后匀速上升6s，最后减速上升3s停止，画出升降机运动过程的速度-时间图象并求：
（1）每一阶段的加速度
（2）每一阶段的平均速度
（3）升降机上升的总高度．
13．一物体以初速度20m/s竖直上抛，当速度大小变为10m/s时所经历的时间可以是（不计空气阻力，g=10m/s2）（　　）
A．1 sB．2 sC．3 sD．4 s

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网