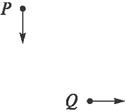题目内容
某空间存在方向垂直于纸面向里的矩形匀强磁场abcd，ad=L，ab=2L．一细束由两种粒子组成的粒子流沿垂直于磁场的方向从ab边的中点O垂直于ad边入射．粒子均带正电荷，它们的电荷量、质量均不同，但其比荷相同，且都包含不同速率的粒子（不计粒子重力）．下列说法正确的是（ ）| A、入射速度不同的粒子在磁场中的运动时间一定不同 | B、入射速度不同的粒子在磁场中的运动时间可能相同 | C、从a点射出的粒子与从b点射出的粒子的运动半径之比为1：17 | D、从a点射出的粒子与从b点射出的粒子的运动半径之比为2：17 |
分析：带电粒子在磁场中由洛伦兹力提供向心力做匀速圆周运动，虽然电量、质量不同，但比荷相同，由r=
，所以运动圆弧对应的半径与速率成正比．由T=
，它们的周期总是相等，因此运动的时间由圆心角来决定．
| mv |
| qB |
| 2πm |
| qB |
解答：
解：A、B、入射速度不同的粒子，它们入射速度方向相同，虽然轨迹不一样，但从磁场的左边射出的粒子，圆心角却相同（θ=π），则粒子在磁场中运动时间：t=
T=
，所以从磁场的左边射出的粒子运动时间一定相同，故A错误，B正确；
C、D、从a点射出的粒子的轨道半径为r1=
；
从b点射出的粒子，结合图中几何关系，有：
=(2L)2+(r2-
)2
解得：r2=
故：r1：r2=1：17
故C正确，D错误；
故选：BC．
解：A、B、入射速度不同的粒子，它们入射速度方向相同，虽然轨迹不一样，但从磁场的左边射出的粒子，圆心角却相同（θ=π），则粒子在磁场中运动时间：t=| 1 |
| 2 |
| πm |
| qB |
C、D、从a点射出的粒子的轨道半径为r1=
| L |
| 4 |
从b点射出的粒子，结合图中几何关系，有：
| r | 2 2 |
| L |
| 2 |
解得：r2=
| 17L |
| 4 |
故：r1：r2=1：17
故C正确，D错误；
故选：BC．
点评：带电粒子在磁场中运动的题目解题步骤为：定圆心、画轨迹、求半径．
练习册系列答案
相关题目
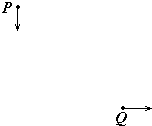空间中存在方向垂直于纸面向里的匀强磁场，磁感应强度为B，一带电量为+q、质量为m的粒子，在P点以某一初速开始运动，初速方向在图中纸面内如图中P点箭头所示．该粒子运动到图中Q点时的速度方向与P点时速度方向垂直，如图中Q点箭头所示．已知P、Q间的距离为l．若保持粒子在P点时的速度不变，而将匀强磁场换成匀强电场，电场方向与纸面平行且与粒子在P点时速度方向垂直，在此电场作用下粒子也由P点运动到Q点．不计重力．求：
