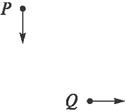题目内容
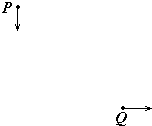 空间中存在方向垂直于纸面向里的匀强磁场,磁感应强度为B,一带电量为+q、质量为m的粒子,在P点以某一初速开始运动,初速方向在图中纸面内如图中P点箭头所示.该粒子运动到图中Q点时的速度方向与P点时速度方向垂直,如图中Q点箭头所示.已知P、Q间的距离为l.若保持粒子在P点时的速度不变,而将匀强磁场换成匀强电场,电场方向与纸面平行且与粒子在P点时速度方向垂直,在此电场作用下粒子也由P点运动到Q点.不计重力.求:
空间中存在方向垂直于纸面向里的匀强磁场,磁感应强度为B,一带电量为+q、质量为m的粒子,在P点以某一初速开始运动,初速方向在图中纸面内如图中P点箭头所示.该粒子运动到图中Q点时的速度方向与P点时速度方向垂直,如图中Q点箭头所示.已知P、Q间的距离为l.若保持粒子在P点时的速度不变,而将匀强磁场换成匀强电场,电场方向与纸面平行且与粒子在P点时速度方向垂直,在此电场作用下粒子也由P点运动到Q点.不计重力.求:(1)电场强度的大小.
(2)两种情况中粒子由P运动到Q点所经历的时间之差.
分析:(1)已知入射速度方向和出射速度方向,由于速度方向始终沿切线方向,故速度方向必与半径垂直,过P点做入射速度的垂线,再过Q点做出射速度的垂线,两垂线交与一点O,则O即是该粒子运动轨迹的圆心.粒子运动了
周,所以PO=QO=R,R为粒子运动半径.又PQ=l,所以R=
(定圆心、找半径)
粒子在磁场中做匀速圆周运动,洛伦兹力充当向心力,故有qv0B=m
,由上述两式可以求出入射速度v0.
把磁场换成与纸面平行且垂直于入射速度v0的电场后,粒子在电场中做类平抛运动,粒子运动到Q点的水平位移x=v0t=R=
,竖直位移y=
×
×t2=R=
,代入数据即可求解.
(2)由题意知粒子在磁场中由P运动到Q用了
周期.轨迹为
圆周.
| 1 |
| 4 |
| l | ||
|
粒子在磁场中做匀速圆周运动,洛伦兹力充当向心力,故有qv0B=m
| ||
| R |
把磁场换成与纸面平行且垂直于入射速度v0的电场后,粒子在电场中做类平抛运动,粒子运动到Q点的水平位移x=v0t=R=
| l | ||
|
| 1 |
| 2 |
| qE |
| m |
| l | ||
|
(2)由题意知粒子在磁场中由P运动到Q用了
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:(1)粒子在磁场中做匀速圆周运动,以v0表示粒子在P点的初速度,R表示圆周半径,则有 qv0B=m
…①
由于粒子在Q点的速度垂直于它在4P点时的速度,可知粒子由P点到Q点的轨迹是圆周的
,
故有 R=
…②
联立①②得:v0=
…③
在电场中粒子做类平抛运动,分别以x、y、E、a、tE表示射程、偏转位移、电场强度,加速度和运动时间,
则:
qE=ma…④
垂直v0方向 y=R=
a
…⑤
沿v0方向 x=R=v0tE…⑥
联立②③④⑤⑥各式可解得:E=
电场强度的大小为:E=
;
(2)由分析知粒子在磁场中由P运动到Q点所经历的时间tB为
周期,
故:tB=
T=
=
在电场中由P运动到Q点所经历的时间tE=
=
由P运动到Q点所经历的时间之差 tB-tE=(
-1)
两种情况中粒子由P运动到Q点所经历的时间之差为(
-1)
| ||
| R |
由于粒子在Q点的速度垂直于它在4P点时的速度,可知粒子由P点到Q点的轨迹是圆周的
| 1 |
| 4 |
故有 R=
| l | ||
|
联立①②得:v0=
| qlB | ||
|
在电场中粒子做类平抛运动,分别以x、y、E、a、tE表示射程、偏转位移、电场强度,加速度和运动时间,
则:
qE=ma…④
垂直v0方向 y=R=
| 1 |
| 2 |
| t | 2 E |
沿v0方向 x=R=v0tE…⑥
联立②③④⑤⑥各式可解得:E=
| 2 |
| qlB2 |
| m |
电场强度的大小为:E=
| 2 |
| qlB2 |
| m |
(2)由分析知粒子在磁场中由P运动到Q点所经历的时间tB为
| 1 |
| 4 |
故:tB=
| 1 |
| 4 |
| 1 |
| 4 |
| 2πR |
| v0 |
| π |
| 2 |
| m |
| qB |
在电场中由P运动到Q点所经历的时间tE=
| R |
| v0 |
| m |
| qB |
由P运动到Q点所经历的时间之差 tB-tE=(
| π |
| 2 |
| m |
| qB |
两种情况中粒子由P运动到Q点所经历的时间之差为(
| π |
| 2 |
| m |
| qB |
点评:带电粒子在垂直磁场射入,粒子将做匀速圆周运动,对于此类问题一般是依照“找圆心,定半径,求时间“来解决.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目