题目内容
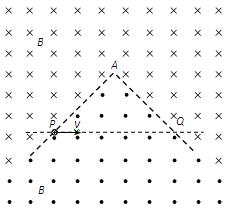
如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.
1.若在P、Q间外加一与磁场方向垂直的匀强电场,能使速度为![]() 射出的微粒沿PQ直线运动到Q点,则匀强电场的场强为多大?
射出的微粒沿PQ直线运动到Q点,则匀强电场的场强为多大?
2.撤去(1)中的匀强电场,为使微粒从P点射出后,途经折线的顶点A而到达Q点,求初速度![]() 应满足什么条件?
应满足什么条件?
3.求第(2)问中微粒从P点到达Q点所用时间的最小值.
1.![]()
2.![]() (
(![]() =1,2,3,…)
=1,2,3,…)
3.![]()
解析:(1)由电场力与洛伦兹力平衡得:![]() ,(2分)则
,(2分)则![]() (2分)
(2分)
(2)根据运动的对称性,微粒能从P点到达Q点,应满足![]() ,
,![]() =1、2、3、…,(2分)
=1、2、3、…,(2分)
其中![]() 为每次偏转圆弧对应的弦长,偏转圆弧对应的圆心角为
为每次偏转圆弧对应的弦长,偏转圆弧对应的圆心角为![]() 或
或![]() . (1分)
. (1分)
设圆弧的半径为R,则有![]() , (1分)
, (1分)
可得:![]() ; (1分) 又,
; (1分) 又, , (1分)
, (1分)
解得:![]() (
(![]() =1,2,3,…) (2分)
=1,2,3,…) (2分)
(3)当![]() 取奇数时,微粒从P到Q过程中偏转圆弧所对应的圆心角的总和为
取奇数时,微粒从P到Q过程中偏转圆弧所对应的圆心角的总和为![]() , (1分)
, (1分)
则![]() ,其中
,其中![]() =1、3、5、… (1分)
=1、3、5、… (1分)
当![]() 取偶数时,微粒从P到Q过程中偏转圆弧所对应的圆心角的总和为:
取偶数时,微粒从P到Q过程中偏转圆弧所对应的圆心角的总和为:![]() , (1分)
, (1分)
则![]() ,其中
,其中![]() =2、4、6、… (1分)
=2、4、6、… (1分)
综合以上n的两种情况,欲使时间最小,取![]() =1或者2,此时都有
=1或者2,此时都有 ![]() .(3分
.(3分

 (2008?淮安模拟)如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.
(2008?淮安模拟)如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力. (2011?陕西二模)如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.
(2011?陕西二模)如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力. 如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.
如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.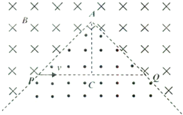 如图所示,空间某平面内有一条折线是磁场的分界线,在折线PAQ的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=
如图所示,空间某平面内有一条折线是磁场的分界线,在折线PAQ的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=