题目内容
 (2008?淮安模拟)如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.
(2008?淮安模拟)如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.(1)若P、Q间外加一与磁场方向垂直的匀强电场,能使速度为v0射出的微粒沿PQ直线运动到Q点,则场强为多大?
(2)撤去电场,为使微粒从P点射出后,途经折线的顶点A而到达Q点,求初速度v应满足什么条件?
(3)求第(2)中微粒从P点到达Q点所用的时间.
分析:(1)根据电场力与洛伦兹力平衡,即可求解;
(2)根据牛顿第二定律,洛伦兹力提供向心力,结合几何关系,即可求解;
(3)由n取奇数与偶数两种情况下,结合圆心角,从而求出时间.
(2)根据牛顿第二定律,洛伦兹力提供向心力,结合几何关系,即可求解;
(3)由n取奇数与偶数两种情况下,结合圆心角,从而求出时间.
解答: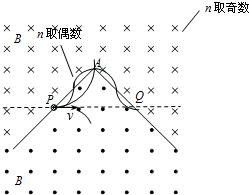 解:
解:
(1)由电场力与洛伦兹力平衡得:qE=qv0B
得:E=v0B
(2)根据运动的对称性,微粒能从P点到达Q点,应满足L=nx
其中x为每次偏转圆弧对应的弦长,偏转圆弧对应的圆心角为
或
.
设圆弧的半径为R,则有2R2=x2,可得:R=
又牛顿第二定律,由洛伦兹力提供向心力,则有:qvB=m
由①②③式得:v=
,n=1、2、3、…
(3)当n取奇数时,微粒从P到Q过程中圆心角的总和为θ1=n?
+n?
=2nπ,
t1=2nπ?
=
?n,其中n=1、3、5、…
当n取偶数时,微粒从P到Q过程中圆心角的总和为θ2=n?
+n?
=nπ
t2=nπ?
=
?n,其中n=2、4、6、…
答:(1)若P、Q间外加一与磁场方向垂直的匀强电场,能使速度为v0射出的微粒沿PQ直线运动到Q点,则场强为E=v0B;
(2)撤去电场,为使微粒从P点射出后,途经折线的顶点A而到达Q点,求初速度v应满足:v=
,n=1、2、3、…
(3)则第(2)中微粒从P点到达Q点所用的时间当n取奇数时,t1=2nπ?
=
?n,其中n=1、3、5、…
当n取偶数时,t2=nπ?
=
?n,其中n=2、4、6、….
 解:
解:(1)由电场力与洛伦兹力平衡得:qE=qv0B
得:E=v0B
(2)根据运动的对称性,微粒能从P点到达Q点,应满足L=nx
其中x为每次偏转圆弧对应的弦长,偏转圆弧对应的圆心角为
| π |
| 2 |
| 3π |
| 2 |
设圆弧的半径为R,则有2R2=x2,可得:R=
| L | ||
|
又牛顿第二定律,由洛伦兹力提供向心力,则有:qvB=m
| v2 |
| R |
由①②③式得:v=
| qBL | ||
|
(3)当n取奇数时,微粒从P到Q过程中圆心角的总和为θ1=n?
| π |
| 2 |
| 3π |
| 2 |
t1=2nπ?
| m |
| qB |
| 2πm |
| qB |
当n取偶数时,微粒从P到Q过程中圆心角的总和为θ2=n?
| π |
| 2 |
| π |
| 2 |
t2=nπ?
| m |
| qB |
| πm |
| qB |
答:(1)若P、Q间外加一与磁场方向垂直的匀强电场,能使速度为v0射出的微粒沿PQ直线运动到Q点,则场强为E=v0B;
(2)撤去电场,为使微粒从P点射出后,途经折线的顶点A而到达Q点,求初速度v应满足:v=
| qBL | ||
|
(3)则第(2)中微粒从P点到达Q点所用的时间当n取奇数时,t1=2nπ?
| m |
| qB |
| 2πm |
| qB |
当n取偶数时,t2=nπ?
| m |
| qB |
| πm |
| qB |
点评:考查受力平衡条件,掌握牛顿第二定律的应用,理解在磁场中运动时间除与圆心角有关外,还与n取奇偶性有关.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2008?淮安模拟)如图所示,足够长的光滑平行金属导轨cd和ef,水平放置且相距L,在其左端各固定一个半径为r的四分之三金属光滑圆环,两圆环面平行且竖直.在水平导轨和圆环上各有一根与导轨垂直的金属杆,两金属杆与水平导轨、金属圆环形成闭合回路,两金属杆质量均为m,电阻均为R,其余电阻不计.整个装置放在磁感应强度大小为B、方向竖直向上的匀强磁场中.当用水平向右的恒力F=
(2008?淮安模拟)如图所示,足够长的光滑平行金属导轨cd和ef,水平放置且相距L,在其左端各固定一个半径为r的四分之三金属光滑圆环,两圆环面平行且竖直.在水平导轨和圆环上各有一根与导轨垂直的金属杆,两金属杆与水平导轨、金属圆环形成闭合回路,两金属杆质量均为m,电阻均为R,其余电阻不计.整个装置放在磁感应强度大小为B、方向竖直向上的匀强磁场中.当用水平向右的恒力F=
 (2008?淮安模拟)矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
(2008?淮安模拟)矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( ) (2008?淮安模拟)北半球海洋某处,地磁场水平分量B1=0.8×10-4T,竖直分量B2=0.5×10-4T,海水向北流动.海洋工作者测量海水的流速时,将两极板竖直插入此处海水中,保持两极板正对且垂线沿东西方向,两极板相距L=20m,如图所示.与两极板相连的电压表(可看作理想电压表)示数为U=0.2mV,则( )
(2008?淮安模拟)北半球海洋某处,地磁场水平分量B1=0.8×10-4T,竖直分量B2=0.5×10-4T,海水向北流动.海洋工作者测量海水的流速时,将两极板竖直插入此处海水中,保持两极板正对且垂线沿东西方向,两极板相距L=20m,如图所示.与两极板相连的电压表(可看作理想电压表)示数为U=0.2mV,则( )