��Ŀ����
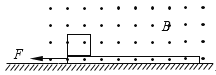
����Ŀ��һ�ΰ���A������ˮƽ��ľ��C�ϣ�������һС���B�����������ڲ�ľ����Ϊ ![]() ����ͼ��ʾ��ľ��λ�ڹ⻬ˮƽ�������ϣ�����ľ����Ħ�����ƣ�С�����ľ����Ħ��ϵ��Ϊ�̣�A��B��C����������ȣ�ԭ������ֹ����ʹ��A�Դ�СΪv0�ij��������˶�����֪v0��
����ͼ��ʾ��ľ��λ�ڹ⻬ˮƽ�������ϣ�����ľ����Ħ�����ƣ�С�����ľ����Ħ��ϵ��Ϊ�̣�A��B��C����������ȣ�ԭ������ֹ����ʹ��A�Դ�СΪv0�ij��������˶�����֪v0�� ![]() ����A��B������ײʱ�������ٶȻ�������
����A��B������ײʱ�������ٶȻ�������
��1����A��B������һ����ײ���ڶ�����ײ��ʱ���ڣ�ľ��C�˶���·������
��2����A��B��Ҫ�������Ĵ���ײʱ��B�ٶȵĴ�С�� ��
���𰸡�
��1��L�� ![]()
��2��![]() v0
v0
���������⣺��1��A��B�շ�����һ����ײ��Aͣ�²�����B�Գ���V0�����˶���
����Ħ����B�������ȼ����˶�����C�������ȼ����˶������������ӽ���
��B��C�ﵽ��ͬ�ٶ�V1ʱB�ƶ���·��ΪS1����A��B��C������Ϊm��������Ϊ������
�ɶ����غ㶨�ɵã�mv0=2mv1����
�������غ㶨�ɵã���mgS1= ![]() 2mv02��
2mv02�� ![]() mv12����
mv12����
�ɢ٢ڽ�ã�S1= ![]()
������֪��v0�� ![]()
��ã�S1�� ![]() L����
L����
�ɼ�����B��C�ﵽ��ͬ�ٶ�v1ʱ��B��δ��A�����ڶ�����ײ��B��Cһ����v1���������˶�һ�ξ��루L��S1�������A�����ڶ�����ײ��
��C���ٶȴ���䵽v1�Ĺ����У�C��·��ΪS2��
�������غ㶨�ɵã���mgS2= ![]() mv12����
mv12����
��ã�S2= ![]()
����ڵ�һ�ε��ڶ�����ײ��C��·��Ϊ��S=S2+L��S1=L�� ![]() ���ݣ���2�����������ۿ�֪���ڸ�Ҫ�����ڶ�����ײʱ��A��ֹ��B��C���ٶȾ�Ϊv1��
���ݣ���2�����������ۿ�֪���ڸ�Ҫ�����ڶ�����ײʱ��A��ֹ��B��C���ٶȾ�Ϊv1��
����ײ��B��ֹ��A��C���ٶȾ�ΪV1������Ħ����B�����٣�C�����٣�ֱ���ﵽ��ͬ�ٶ�v2��
������Ϊ�������ɶ����غ㶨�ɵã�mv1=2mv2����
��ã�v2= ![]() v1=
v1= ![]() v0
v0
��A���ٶ�v1����B���ٶ�v2���ʵ�������ײ������A����ڣ�
����ײ��A���ٶȱ�ΪV2��B���ٶȱ�ΪV1��C���ٶ���ΪV2��
����Ħ����B���٣�C���٣�ֱ���ﵽ��ͬ�ٶ�v3����A���ٶȷ���Ϊ������
�ɶ����غ㶨�ɵã�mv1+mv2=2mv3����
��ã�v3= ![]() v0
v0
�ʸ�Ҫ�������Ĵ���ײʱ��A��B��C���ٶȷֱ�Ϊ��vA=v2= ![]() v0����
v0����
vB=vC=v3= ![]() v0����
v0����
���Դ��ǣ���1��L�� ![]() ����2��
����2�� ![]() v0��
v0��
�����㾫����������Ŀ����֪���������ö����غ㶨�ɵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣮