题目内容
【题目】如图所示，半径为R的四分之三圆周CED，O为圆心，A为CD的中点，在OCEDO内充满垂直于纸面向外的匀强磁场(图中未画出)，磁感应强度大小为B.一群相同的带正电粒子以相同的速率从AC部分垂直于AC射向磁场区域，沿半径OD放置一粒子吸收板，所有射在板上的粒子均被完全吸收．已知粒子的质量为m，电量为q，速率v＝
，假设粒子不会相遇，忽略粒子间的相互作用，不考虑粒子的重力．求：
(1)粒子在磁场中的运动半径；
(2)粒子在磁场中运动的最短和最长时间；
(3)吸收板上有粒子击中的长度．
【答案】（1）
（2）
（3）
【解析】(1)由qvB＝m
代入v得r＝
(2)粒子在磁场中做圆周运动的周期为T，则有
如图所示，部分粒子从OC边射入磁场，又从OC边射出磁场
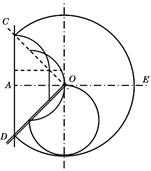
由对称性可知，粒子偏转的圆心角为90°，最短时间
沿AO入射的粒子，与磁场圆在最低点内切，圆心角为270°，如图所示最长时间
(3)轨迹圆圆心的轨迹一定在与OC平行的线上，如图中O1、O2、O3线上，
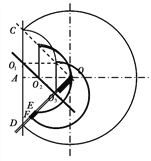
其中O1在AC上，O2在OA上，O3在板OD上
①圆心在O1到O2间时，粒子打在板OD的左面，由图中几何关系得，左表面的长度范围为
L1＝R－
R＝
R
②圆心在O2到O3间时，粒子打在板OD的右面，由图中几何关系得，右表面的长度范围为EF段，长度为L2＝
－
R＝
R
综上，有粒子击中的长度为L＝L1＋L2＝
R－
R＝
R
【题目】伽利略在《两种新科学的对话》一书中，提出猜想：物体沿斜面下滑是一种匀变速直线运动，同时他还用实验验证了该猜想。某小组依据伽利略描述的实验方案，设计了如图所示的装置，探究物体沿斜面下滑是否做匀变速直线运动。实验操作步骤如下：
①让滑块从距离挡板s处由静止沿倾角为θ的斜面下滑，并同时打开装置中的阀门，让水箱中的水流到量筒中；
②当滑块碰到挡板的同时关闭阀门(假设水流均匀稳定)；
③记录下量筒收集的水量V；
④改变s，重复以上操作；
⑤将测得的数据记录在表格中。
次数 | 1 | 2 | 3 | 4 | 5 | 6 |
s/m | 4.5 | 3.9 | 3.0 | 2.1 | 1.5 | 0.9 |
V/mL | 90 | 84 | 62 | 52 | 40 |
(1)该实验用量筒中收集的水量来表示________。
A．水箱中水的体积 B．水从水箱中流出的速度
C．滑块下滑的时间 D．滑块下滑的位移
(2)某同学漏填了第3组数据中量筒收集的水量V，若实验正常，你估计V＝________mL；若保持下滑的距离s、倾角θ不变，增大滑块的质量，水量V将________(填“增大”“不变”或“减小”)；若保持下滑的距离s、滑块质量不变，增大倾角θ，水量V将________(填“增大”“不变”或“减小”)。
(3)下列说法中不属于该实验误差来源的是________。
A．水从水箱中流出不够稳定
B．滑块开始下滑和开始流水不同步
C．选用的斜面不够光滑
D．选用了内径较大的量筒
