��Ŀ����
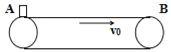
����Ŀ����ͼ��ʾ��ˮƽ���ʹ�A��B���˵����x=4m����v0=2m/s���ٶȣ�ʼ�ձ��ֲ��䣩˳ʱ����ת����һ����Ϊ1kg��Сú�飨����Ϊ�ʵ㣩���ٶ�����ŵ�A�㴦����֪Сú���봫�ʹ���Ķ�Ħ������Ϊ0.4��gȡ10m/s2������Сú���봫�ʹ�֮������Ի��������ڴ��ʹ������»��ۣ���Сú���A�˶���B�Ĺ����У�������
A. Сú���˶���B���ٶȴ�СΪ4![]() m/s
m/s
B. Сú���A�˶���B��ʱ��Ϊ2.25s
C. ���۳���Ϊ1m
D. Сú���봫�ʹ�ϵͳ����������Ϊ2J
���𰸡�BD
��������Сú���˶���B���ٶȲ����ܳ������ʹ����ٶȣ���������Ϊ4![]() m/s����A����Сú���ȼ��ٺ����٣�����ţ�ٵڶ����ɣ��ã�a=
m/s����A����Сú���ȼ��ٺ����٣�����ţ�ٵڶ����ɣ��ã�a= ![]() =0.4��10=4m/s2��
=0.4��10=4m/s2��
����ʱ��Ϊ��t1=![]() =0.5s��
=0.5s��
����λ�ƣ� ![]() ��
��
����ʱ�䣺 ![]() ��
��
���˶�����ʱ��Ϊ��t=t1+t2=0.5s+1.75s=2.25s����B��ȷ��
�ڼ��ٹ��̣����ʹ���λ��Ϊ��x1��=v0t1=2��0.5=1m���ʻ���Ϊ�� ![]() =1��0.5=0.5m����C����Сú���봫�ʹ�ϵͳ����������Ϊ��Q=f��x=��mg��x=0.4��1��10��0.5=2J����D��ȷ����ѡBD.
=1��0.5=0.5m����C����Сú���봫�ʹ�ϵͳ����������Ϊ��Q=f��x=��mg��x=0.4��1��10��0.5=2J����D��ȷ����ѡBD.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ijͬѧ��������װ�ö����ʵ��ɵĵ������ܽ���̽����һ���ʵ��ɷ����ڹ⻬ˮƽ�����ϣ�������˹̶����Ҷ���һС��Ӵ��������������ɴ���ԭ��ʱ��С��ǡ���������Ե����ͼ��a����ʾ��������С��ʹ����ѹ��һ�ξ�����ɾ�ֹ�ͷţ�С���뿪������䵽ˮƽ���森ͨ�������ͼ��㣬����õ��ɱ�ѹ����ĵ������ܣ��ش��������⣺
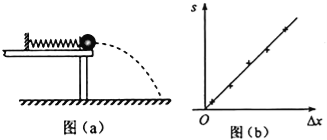
��1����ʵ���п���Ϊ�����ɱ�ѹ����ĵ�������Ep��С���׳�ʱ�Ķ���Ek��ȣ���֪�������ٶȴ�СΪg��Ϊ���Ek��������Ҫ���������������е� ������ȷ�𰸱�ţ���
A���������m |
B��С���׳��㵽��ص��ˮƽ����s |
C�����浽����ĸ߶�h |
D�����ɵ�ѹ������x |
E������ԭ��l0
��2������ѡȡ�IJ���������֪����ʾEk����Ek= ��
��3��ͼ��b���е�ֱ����ʵ������õ���s����xͼ�ߣ��������Ͽ��Ƴ������h���䣮m���ӣ�s����xͼ�ߵ�б�ʻ� ������������������С�������������������m���䣬h���ӣ�s����xͼ�ߵ�б�ʻ� ������������������С������������������ͼ��b�� �и�����ֱ�߹�ϵ��Ek�ı���ʽ��֪��Ep����x�� �η������ȣ�