题目内容
19.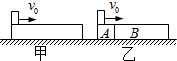 将一长木板静止放在光滑的水平面上,如图甲所示,一个滑块(可视为质点)以水平速度v0从木板左端向右端滑动,到达右端时恰能与木板保持相对静止.现将木板分成A和B两段,如图乙所示,并紧挨着放在水平面上,让滑块仍以初速度v0从从木板左端向右端滑动.滑块与木板的动摩擦因数处处相同,在以后的整个过程中,则下列说法正确的是( )
将一长木板静止放在光滑的水平面上,如图甲所示,一个滑块(可视为质点)以水平速度v0从木板左端向右端滑动,到达右端时恰能与木板保持相对静止.现将木板分成A和B两段,如图乙所示,并紧挨着放在水平面上,让滑块仍以初速度v0从从木板左端向右端滑动.滑块与木板的动摩擦因数处处相同,在以后的整个过程中,则下列说法正确的是( )| A. | 甲、乙两图中,滑块克服摩擦力做的功一样多 | |
| B. | 系统因摩擦产生的热量甲图比乙图多 | |
| C. | 若B的质量越大,则滑块与木板从开始到共速经历的时间会越长 | |
| D. | 若B的质量越小,则系统因摩擦产生的热量会越大 |
分析 比较两次运动的区别,木块一直做匀减速直线运动,木板一直做匀加速直线运动,第一次在小滑块运动过程中,整个木板一直加速,第二次小滑块运动的过程中,A与B先一起做加速运动,当滑块运动到B部分上后A部分停止加速做匀速直线运动,只有B部分加速,B的加速度大于开始时的加速度,通过比较小滑块的位移确定是否飞离木板.(也可以使用动能定理比较).
根据摩擦力乘以相对位移等于热量比较小滑块在木板B上和木板A上产生的热量.
解答 解:设滑块的质量为m,A部分的质量为M1,B的质量为M2,则滑块在木板上运动的过程中,系统的动量守恒,选择向右为正方向,对甲图:
mv0=(m+M1+M2)v…①
对乙图,则:mv0=M1v1+(m+M2)v2…②
由于滑块滑过A后,在B上滑动的过程中,滑块的速度将大于A的速度,所以可得:
v1<v<v2
可知第二次时滑块的速度的变化量小一些,根据动量定理可知,滑块与B木板将比第一种的情景更早达到速度相等,所以在第二种的情况下,滑块还没有运动到B的右端,两者速度相同,即第二次时,滑块相对于木板的位移小.
A、根据动能定理可知,滑块克服摩擦力做的功等于其动能的变化,由于v<v2,所以甲、乙两图中,滑块克服摩擦力做的功不一样多.故A错误;
B、根据摩擦力乘以相对位移等于产生的热量,第一次的相对路程的大小 大于第二次的相对路程的大小,则图甲所示的过程产生的热量大于图乙所示的过程产生的热量.故B正确;
C、在滑块的质量与木板的质量一定的条件下,B在质量越大,则长度越长,滑块与A分离的越早,由②可知,滑块与B的共同速度越大,则滑块与木板从开始到共速经历的时间$t=\frac{m{v}_{0}-m{v}_{2}}{f}$会越短.故C错误;
D、由紧逼法来思考:设木块的质量为M,其中A部分的质量为M1,B部分的质量为M2,那么在M2无限趋近于M时和M2无限趋近于零时,(系统因摩擦产生的热量)与第一次小滑块运动时也几乎相同.故D错误.
故选:B
点评 解决本题的关键理清滑块和木板的运动过程,通过比较位移的关系判断是否脱离,以及掌握功能关系Q=fs相对.

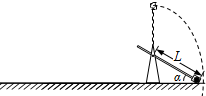 “抛石机”是古代战争中常用的一种设备,如图所示.某研究小组用自制的抛石机演练抛石过程:所用抛石机长臂的长度L,石块装在长臂末端的口袋中.开始时长臂与水平面间的夹角为α,现对短臂施力,使石块经较长路径获得较大的速度,当长臂转到竖直位置时立即停止转动,石块被水平抛出,石块落地位置与抛出位置间的水平距离为s.不计空气阻力,重力加速度已知,根据以上条件,不能求出的物理量是( )
“抛石机”是古代战争中常用的一种设备,如图所示.某研究小组用自制的抛石机演练抛石过程:所用抛石机长臂的长度L,石块装在长臂末端的口袋中.开始时长臂与水平面间的夹角为α,现对短臂施力,使石块经较长路径获得较大的速度,当长臂转到竖直位置时立即停止转动,石块被水平抛出,石块落地位置与抛出位置间的水平距离为s.不计空气阻力,重力加速度已知,根据以上条件,不能求出的物理量是( )| A. | 抛石机对石块所做的功 | B. | 石块刚抛出时的速度大小 | ||
| C. | 石块刚落地时的速度大小 | D. | 石块刚落地时的速度方向 |
 滑滑梯是小朋友特别喜欢的游乐项目之一,我市青枫公园儿童游乐区有这么一种滑梯,它由两个不同倾角的滑梯构成,两名儿童可同时从顶端滑下进行竞速比赛.若两名儿童的体重相同,不考虑滑梯的摩擦,則下列说法中正确的是( )
滑滑梯是小朋友特别喜欢的游乐项目之一,我市青枫公园儿童游乐区有这么一种滑梯,它由两个不同倾角的滑梯构成,两名儿童可同时从顶端滑下进行竞速比赛.若两名儿童的体重相同,不考虑滑梯的摩擦,則下列说法中正确的是( )| A. | 两人下滑过程中重力做功相等 | |
| B. | 两人到达斜面底端时的动能相等 | |
| C. | 两人下滑过程中重力的平均功率相等 | |
| D. | 两人到达斜面底端时所受重力的瞬时功率相等 |
 在三维直角坐标系中,电子沿y轴正方向运动,如图所示,由于电子的运动产生的磁场在a点的方向是( )
在三维直角坐标系中,电子沿y轴正方向运动,如图所示,由于电子的运动产生的磁场在a点的方向是( )| A. | +x方向 | B. | -x方向 | C. | +z方向 | D. | -z方向 |
 如图所示,圆锥摆的摆长为L、摆角为α,质量为m的摆球在水平面内做匀速圆周运动,则( )
如图所示,圆锥摆的摆长为L、摆角为α,质量为m的摆球在水平面内做匀速圆周运动,则( )| A. | 摆线的拉力为$\frac{mg}{cosα}$ | B. | 摆球的向心加速度为gcosα | ||
| C. | 其运动周期为2π$\sqrt{\frac{L}{g}}$ | D. | 其运动周期为2π$\sqrt{\frac{Lcosα}{g}}$ |
| A. | 上海磁悬浮列车的最高速度可达430km/h,它的加速度一定很大 | |
| B. | 运载火箭在点火后的短时间内,速度的变化很小,它的加速度也很小 | |
| C. | 优秀短跑运动员起跑后,速度可以在0.1s内达到10m/s,说明他的加速度小,但速度变化得快 | |
| D. | 枪膛中的子弹初速度为零,加速度却很大,是由于子弹在短时间内速度改变得很多 |
| A. | 研究某细胞的有丝分裂 | |
| B. | 研究人随地球自转情况 | |
| C. | 研究一列火车从三明开到北京所用的时间 | |
| D. | 研究2012年伦敦奥运会上我国女单选手李晓霞乒乓球的旋转 |
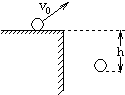 如图所示,在水平台面上的A点,一个质量为m的物体以v0抛出不计空气阻力,从A到B的过程中物体的机械能守恒,到B点时速度大小为$\sqrt{{v}_{0}^{2}+2gh}$.
如图所示,在水平台面上的A点,一个质量为m的物体以v0抛出不计空气阻力,从A到B的过程中物体的机械能守恒,到B点时速度大小为$\sqrt{{v}_{0}^{2}+2gh}$. 一列简谐横波在x轴上传播,M、N是x轴上相距7m的两质点,当时间t=0时,N点正好到达最高点,且N点到x轴的距离为3cm,而此时M点恰好经过平衡位置向上移动,已知这列波的频率为25Hz.
一列简谐横波在x轴上传播,M、N是x轴上相距7m的两质点,当时间t=0时,N点正好到达最高点,且N点到x轴的距离为3cm,而此时M点恰好经过平衡位置向上移动,已知这列波的频率为25Hz.