Question

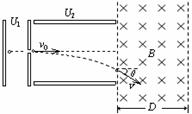
(10分)如图所示，一个质量为m =2.0×10^-11kg，电荷量q = +1.0×10^-5C的带电微粒（重力忽略不计），从静止开始经U₁=100V电压加速后，水平进入两平行金属板间的偏转电场，偏转电场的电压U₂=100V。金属板长L=20cm，两板间距d =cm。求：

（1）微粒进入偏转电场时的速度v₀大小；

（2）微粒射出偏转电场时的偏转角θ；

（3）若该匀强磁场的宽度为D=10cm，为使微粒不会由磁场右边射出，该匀强磁场的磁感应强度B至少多大？

Answer 1

(15分)解：（1）微粒在加速电场中由动能定理得：

qu₁=mv₀²/2 ①        解得v₀=1.0×104m/s   ……3分

（2）微粒在偏转电场中做类平抛运动，有： a=qu₂/md，v_y=at=aL/ v₀   ……2分

飞出电场时，速度偏转角的正切为：

tanθ=v_y/v₀=U₂L/2dU₁=1/(3)^1/2②  解得  θ=30o   ……3分

（3）进入磁场时微粒的速度是： v=v₀/cosθ    ③……2分

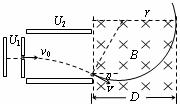
轨迹如图，由几何关系有：  ④    ……2分

洛伦兹力提供向心力：   Bqv=mv²/r      ⑤

由③～⑤联立得： B=mv₀(1+sinθ)/qDcosθ  代入数据解得：

B ＝3^1/2/5=0.346T  ……2分

所以，为使微粒不会由磁场右边射出，该匀强磁场的磁感应强度B至少为0.346T。